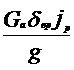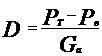Для переднего моста
| (1.59) |
Для заднего моста
| (1.60) |
Рассуждая аналогично, можно определить реакции и коэффициенты изменения реакций для ТС со всеми ведущими колесами. В случае переднего ведущего моста
| (1.61) |
При разгоне автомобиля наибольшее значение коэффициентов изменения реакций находятся в следующих пределах:
для переднего моста ![]() =0,65-0,7;
=0,65-0,7;
для переднего моста ![]() =1,2-1,35.
=1,2-1,35.
§2. Уравнение движения транспортных средств
Одновременное рассмотрение движущихся сил и сил сопротивления движению позволяет составить уравнение движения ТС.
При прямолинейном движении ТС преодолевает силу сопротивления движению ![]() , которая представляет собой сумму сил сопротивления дороги, воздуха и сил инерции.
, которая представляет собой сумму сил сопротивления дороги, воздуха и сил инерции.
Все силы сопротивления преодолеваются за счет тяговой силы ![]() на ведущих колесах ТС:
на ведущих колесах ТС:
| (1.62) |
или
| (1.63) |
Полученное уравнение называется уравнением силового баланса ТС. На рис. 1.6. приведен график силового баланса ТС.
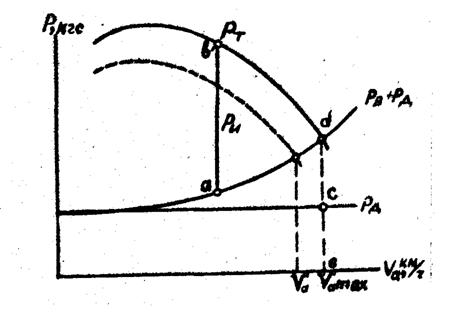
Рис. 1.6. График силового баланса ТС и сил сопротивления воздуха и дороги.
В координатах ![]() -
-![]() построены кривые зависимости силы тяги от скорости движения на передачах и кривые, характеризующие силы сопротивления дороги и воздуха. Значение силы сопротивления воздуха отложены вверх от прямой
построены кривые зависимости силы тяги от скорости движения на передачах и кривые, характеризующие силы сопротивления дороги и воздуха. Значение силы сопротивления воздуха отложены вверх от прямой ![]() .
.
При любой скорости равномерного движения тяговая сила ![]() равна сумме всех сил сопротивления. Отрезок
равна сумме всех сил сопротивления. Отрезок ![]() -
-![]() между кривыми
между кривыми ![]() и
и ![]() +
+![]() характеризует «запас», который может быть использован для ускорения ТС. Точка
характеризует «запас», который может быть использован для ускорения ТС. Точка ![]() пересечения указанных кривых – переход автомобиля от ускоренного движения к равномерному со скоростью
пересечения указанных кривых – переход автомобиля от ускоренного движения к равномерному со скоростью ![]() , максимально возможной в данных дорожных условиях. Величина отрезка
, максимально возможной в данных дорожных условиях. Величина отрезка ![]() -
-![]() характеризует силу сопротивления воздуха, а отрезок
характеризует силу сопротивления воздуха, а отрезок ![]() -
-![]() -силу сопротивления дороги при движении ТС с максимальной скоростью.
-силу сопротивления дороги при движении ТС с максимальной скоростью.
Разность тяговой силы и силы сопротивления воздуха (![]() -
-![]() ) называется избыточной силой тяги, которая идет на преодоление сопротивления дороги и разгон (рис.1.7.)
) называется избыточной силой тяги, которая идет на преодоление сопротивления дороги и разгон (рис.1.7.)
Если от кривой ![]() отложить вниз отрезки, соответствующие значениям сил сопротивления воздуха при различных скоростях движения, и через концы этих отрезков провести кривую, то эта кривая будет характеризовать избыточную силу тяги
отложить вниз отрезки, соответствующие значениям сил сопротивления воздуха при различных скоростях движения, и через концы этих отрезков провести кривую, то эта кривая будет характеризовать избыточную силу тяги ![]() -
-![]() . Проведя затем на том же графике горизонтали, соответствующие различным величинам сил сопротивления дороги
. Проведя затем на том же графике горизонтали, соответствующие различным величинам сил сопротивления дороги ![]() , можно определить силу
, можно определить силу ![]() , затраченную на разгон ТС. Графически сила изображена в виде отрезка между кривой избыточной силы
, затраченную на разгон ТС. Графически сила изображена в виде отрезка между кривой избыточной силы ![]() -
-![]() и горизонталью
и горизонталью ![]() . Чем меньше сопротивление дороги, тем с большим ускорением может двигаться ТС.
. Чем меньше сопротивление дороги, тем с большим ускорением может двигаться ТС.
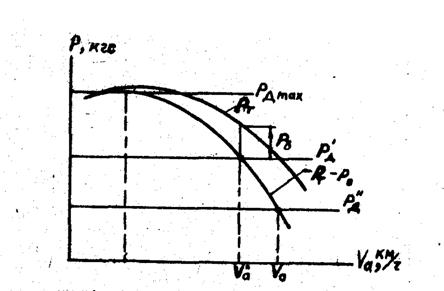
Рис.1.7. График силового баланса ТС и избыточной силы
При движении с установившейся скоростью вся избыточная сила тяги расходуется на преодоление сопротивления дороги:
| (1.64) |
Ординаты кривой избыточной силы тяги определяют собой максимальные величины сил сопротивления дороги, которые ТС может преодолеть на этих скоростях при полностью открытой дроссельной заслонке.
Для малых углов 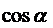
![]() 1,
1, ![]() =
=![]() +
+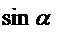
отсюда угол подъема
| (1.65) |
Максимальное сопротивление дороги преодолевается при наибольшем значении избыточной силы тяги. Чтобы найти это значение, нужно провести горизонтальную прямую ![]() , касательную к кривой
, касательную к кривой ![]() -
-![]() в точке ее перегиба. Ордината точки касания дает максимальные значения избыточной силы тяги.
в точке ее перегиба. Ордината точки касания дает максимальные значения избыточной силы тяги.
Динамическая характеристика ТС[2]
Если два ТС разной массы развивают одинаковую избыточную тяговую силу, то тяговые качества будут выше у более легкого ТС. Поэтому удобнее измерять динамичность ТС с помощью отношения избыточной силы тяги к его полной массе. Этот показатель был предложен и назван динамическим фактором :
| (1.66) |
Если на графике отложить величину динамического фактора на каждой передаче в зависимости от скорости, получим динамическую характеристику ТС (рис.1.8). Число кривых на этом графике равно числу передач в трансмиссии ТС.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 |




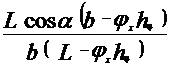
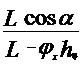
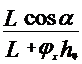
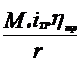 =
=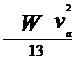 +
+