| (3.19) |
Степень величины, входящих в формулу (3.15), показывает, что для большинства транспортных автомобилей при эксплуатационных режимах движения значения сил ![]() и
и ![]() не превышают 3-5% величины силы
не превышают 3-5% величины силы ![]() . Поэтому в основном без заметной ошибки поперечную силу можно рассчитывать по формуле (3.19). исключение составляют лишь автомобили, движущиеся с очень высокими скоростями (спортивные, гоночные) по кривым переменного радиуса, требующим резкого поворота рулевого колеса.
. Поэтому в основном без заметной ошибки поперечную силу можно рассчитывать по формуле (3.19). исключение составляют лишь автомобили, движущиеся с очень высокими скоростями (спортивные, гоночные) по кривым переменного радиуса, требующим резкого поворота рулевого колеса.
Скольжение шин по дороге начинается в тот момент, когда горизонтальная сила, действующая на автомобиль, достигнет значения силы сцепления. Если продольные силы в зонах контакта шин с дорогой отсутствуют, то сцепление шин с дорогой используется только в поперечном направлении. В этом случае сила сцепления шин всех колес автомобиля.
| (3.20) |
Сопоставив выражения (3.19) и (3.20), найдем величину критической скорости автомобиля по условиям поперечного скольжения (заноса):
| (3.21) |
Эта формула действительна при условии, что продольные силы в зонах контакта шин с дорогой отсутствуют, а автомобиль движется равномерно по кривой постоянного радиуса. В реальных условиях автомобиль весьма редко движется по кривой постоянного радиуса, тем более при ДТП.
Если при прямолинейном движении (![]() =
=![]() ) на горизонтальной проезжей части с постоянной скоростью (
) на горизонтальной проезжей части с постоянной скоростью (![]() =0) водитель резко поворачивает рулевое колесо, то в начальный момент сила
=0) водитель резко поворачивает рулевое колесо, то в начальный момент сила ![]() отсутствует. В этом случае на автомобиль действует сила
отсутствует. В этом случае на автомобиль действует сила ![]() , и скольжение наступает, если
, и скольжение наступает, если
| (3.22) |
откуда предельная скорость, при которой может наступить занос автомобиля,
| (3.23) |
Таким образом, занос автомобиля может быть и при прямолинейном движении, если водитель достаточно резко повернет рулевое колесо.
Автомобиль, движущийся прямолинейно (рис.3.2, участок АВ), не может мгновенно перейти на кривую СД постоянного радиуса, так как для этого необходимо повернуть управляемые колеса с бесконечно большой скоростью (![]()
![]()
![]() ). Поэтому между прямолинейным участком дороги и круговой кривой обязательно должен быть переходной участок ВС переменной кривизны.
). Поэтому между прямолинейным участком дороги и круговой кривой обязательно должен быть переходной участок ВС переменной кривизны.
Под действием поперечной силы может произойти также опрокидывание ТС. Если боковые силы приложены выше зоны контакта шин с дорогой и скольжение колес не происходит, то опрокидывание может начаться без предшествующего заноса.
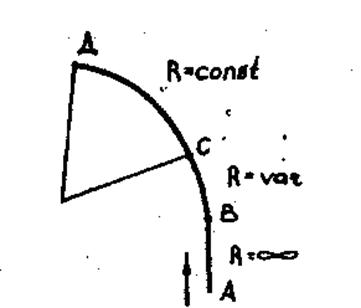
Рис.3.2. схема входа автомобиля в поворот постоянного радиуса
Если автомобиль движется на повороте с постоянным радиусом и скоростью по горизонтальной дороге и на него не действуют никакие другие боковые силы, кроме центробежной (рис.3.3), то его предельная скорость (в километрах в час), при которой не исключается опрокидывание, определяется по формуле
| (3.24) |
где ![]() - коэффициент, учитывающий поперечный крен подрессорных масс вследствие деформации упругих элементов подвески (рессор, пружин, торсионов и шин. В среднем
- коэффициент, учитывающий поперечный крен подрессорных масс вследствие деформации упругих элементов подвески (рессор, пружин, торсионов и шин. В среднем ![]() =0,8-0,9.
=0,8-0,9.
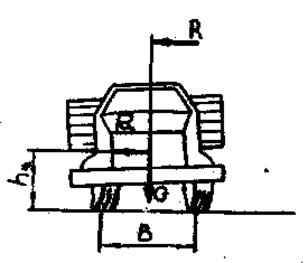
Рис. 3.3. Схема сил, действующих на автомобиль при повороте
В процессе движения колеса автомобиля могут наезжать на дорожные неровности или ударяться о них. При этом могут возникать боковые силы, вызывающие отрыв колес от поверхности дороги и поворот их и приводящие как следствие, к потере автомобилем устойчивости и управляемости.
Причиной возникновения момента, поворачивающегося автомобиль в горизонтальной плоскости, могут быть различные силы сцепления с дорожным покрытием с правой и левой стороны автомобиля.
Так, и если автомобиль движется по дороге, по ширине которой коэффициент сцепления имеет разные значения, или на автомобиле установлены шины с неодинаковой степенью износа рисунка протектора, то может возникнуть поворачивающий момент. Особенно опасна разница в коэффициентах сцепления при торможении, когда продольные силы и поворачивающий момент достигают больших значений.
При торможении автомобиля момент также возникать из-за неодинаковых по сторонам автомобиля зазоров между тормозными накладками и барабанами, из-за замасливания трущихся поверхностей. Различные по величине тормозные моменты на колесах правой и левой стороны автомобиля вызывают появление поворачивающего момента.
Если, например, коэффициент сцепления ![]() с правой стороны автомобиля больше коэффициента
с правой стороны автомобиля больше коэффициента ![]() с левой стороны, то величина поворачивающего момента (рис. 3.4.) при полном использовании сцепления
с левой стороны, то величина поворачивающего момента (рис. 3.4.) при полном использовании сцепления
| (3.25) |
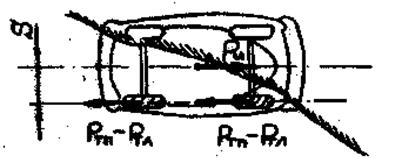
Рис. 3.4. Схема торможения при разных тормозных силах
Под действием момента ![]() автомобиль приобретает угловое ускорение
автомобиль приобретает угловое ускорение ![]() :
:
| (3.26) |
где ![]() - момент инерции автомобиля относительно вертикальной оси, проходящей через его центр тяжести, кгс∙м∙с².
- момент инерции автомобиля относительно вертикальной оси, проходящей через его центр тяжести, кгс∙м∙с².
Угол поворота автомобиля
| (3.27) |
Угол ![]() максимален в том случае, когда граница между участками дороги с различными значениями
максимален в том случае, когда граница между участками дороги с различными значениями ![]() проходит через центр тяжести автомобиля. Для грузового автомобиля и автобуса
проходит через центр тяжести автомобиля. Для грузового автомобиля и автобуса
| (3.28) |
для легкового

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 |




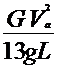 =
=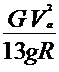
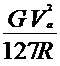 .
.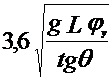 =
=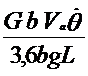 ,
,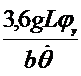
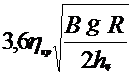 ,
,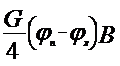
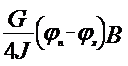
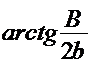 ,
,