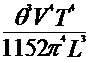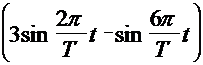Смещение автомобиля по ширине проезжей части в конце маневра должно быть достаточно велико, чтобы избежать наезда на препятствие и обеспечить необходимый интервал (траектория должна отличаться от кривой IY), но автомобиль при этом должен оставаться в пределах проезжей части (траектория должна отличаться от кривой III). Кроме того, водитель должен выполнить маневр за минимальное время, а ТС сохранить устойчивость.
При такой смене полосы движения в аварийных ситуациях закон изменения угла поворота управляемых колес 
по времени 
близок к синусоидальному (рис. 4.2) и может быть выражен формулой
| (4.1) |
.Скорость поворота управляемых колес
| (4.2) |
= 
,где 
- максимальный угол поворота колес (точка над символом означает производную по времени);
- частота;
- период; 
=
.
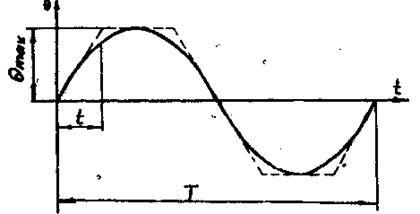
Рис. 4.2. График изменения угла поворота управляемых колес по времени
При исследовании эксплуатационных свойств автомобиль заменяется расчетной моделью. Вначале рассмотрим наиболее простую модель, полагая, что автомобиль является плоской фигурой, шины абсолютно жесткие в поперечном направлении, а рулевая трапеция обеспечивает необходимые соотношения углов поворота управляемых колес. Если закон поворота управляемых колес по времени выражен формулой (4.1), то
| (4.3) |
.где 
- расстояние от середины заднего моста ТС до мгновенного центра скоростей («радиус поворота»), м.
Для малых углов
| (4.4) |
.Пусть в начальный момент поворота середина заднего моста (рис.4., точка В) автомобиля совпала с началом координат XOY.
Рис. 4.3. Схема поворота автомобиля с жесткими шинами
В некоторый момент времени продольная ось маневрирующего автомобиля составит с прежнем направлением движения угол 
. После поворота еще на бесконечно малый угол 
точка B опишет дугу, длина которой равна:
|
При равномерном движении со скоростью 
(в метрах в секунду)
|
.Следовательно,
| (4.5) |
=
Подставив в эту формулу значения из выражения (4.4), после интегрирования найден угол, на который отклоняется продольная ось автомобиля за время :
| (4.6) |
=
.или, выразив частоту через период , получим
| (4.7) |
.По этому выражению можно найти величину курсового угла в любой момент времени.
Спроектировав дугу 
на оси координат, получим приращения координат X и Y точки B:
| (4.8) |
=
=
| (4.9) |
=
=После подстановки в формулы (4.8) и (4.9) значения угла согласно формуле (4.7) уравнения, не решаемые в элементарных функциях. Поэтому представим 
и 
в виде функции двух углов. После разложения их в ряд Тейлора, пренебрегая величинами четвертой степени малости и выше, имеем:
+ + + | (4.10) |
+
+
+
- - - | (4.11) |
По формулам (4.7) - (4.11) можно определить значение курсового угла и координат 
и 
середины заднего моста автомобиля для любого момента времени и построить траекторию движения ТС. При выполнении маневра траектория движения автомобиля может быть различной, так как величину максимального поворота нельзя выбирать произвольно. Она может быть ограничена следующими факторами:
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 |
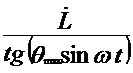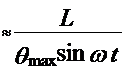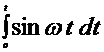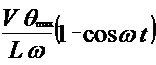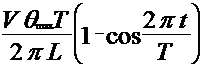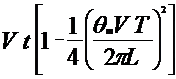
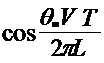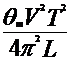
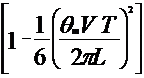
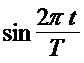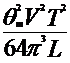
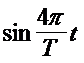