=- - - ;

(4.70)

=+- - ;

(4.71)

=- - - .

(4.72)

где - масса автомобиля;

, - ускорения центра тяжести автомобиля соответственно в направлении осей X и Y;

, - суммарные касательные реакции, действующие на оба колеса соответственно передней и задней оси автомобиля;

, - суммарные боковые реакции, действующие на оба колеса соответственно передней и задней осей автомобиля;

, - суммы проекций на оси X и Y внешних сил, действующих на автомобиль;

- момент инерции автомобиля относительно оси Z;

- угловое ускорение автомобиля относительно оси Z;

, - расстояния от центра тяжести автомобиля соответственно до передней и задней осей;

- сумма внешних моментов, действующих на автомобиль относительно оси Z.

Входящие в эти уравнения боковые реакции и могут быть выражены через углы увода, а между углами увода и , с одной стороны, и ускорениями и, с другой, существует определенная зависимость. Поэтому неизвестные величины и , и могут быть выражены через какую-либо пару неизвестных, однозначно связанных с углами увода или ускорениями.

Положение автомобиля относительно неподвижной системы координат можно характеризовать текущими координатами опорной точки и курсовым углом продольной оси (рис. 4.9). Для экспертного исследования за опорную точку целесообразно выбрать середину заднего моста автомобиля, расстояние от которой до любой точки ТС можно получить на масштабном плане. При экспериментальной проверке теоретических результатов к середине заднего моста конструктивно удобно крепить необходимое оборудование.

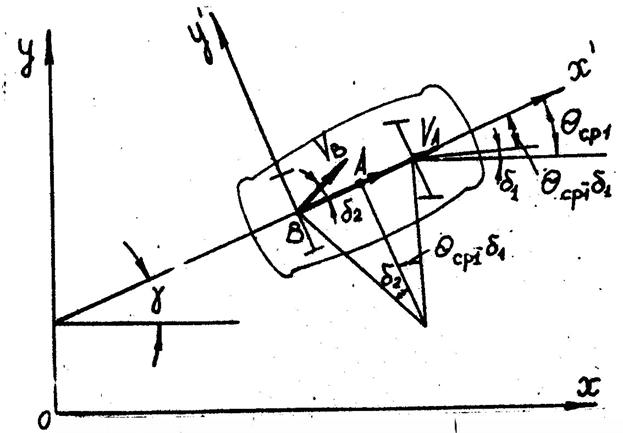
Рис.4.9. Схема поворота автомобиля в подвижной и неподвижной

системах координат:

- вектор скорости поступательного движения центра тяжести автомобиля; - вектор скорости середины заднего моста; , - углы увода середин переднего и заднего мостов; - курсовой угол автомобиля

Проекция вектора скорости середины заднего моста на неподвижные оси OX и OY неподвижной системы координат могут быть выражены следующим образом[21]:

=-;

(4.73)

=+;

(4.74)

Угловая скорость автомобиль равна:

=≈.

(4.75)

Для получения траектории автомобиля необходимо рассчитать текущие координаты опорной точки относительно необходимых осей X и Y. Эти координаты могут быть получены путем интегрирования уравнений по времени:

=+;

(4.76)

=+;

(4.77)

где , - постоянные, определяемые по начальным условиям.

Аналогично из выражения (4.72) можно определить курсовой угол

==+.

(4.78)

Таким образом, расчет траектории движения и курсового угла может быть произведен, если известны закон поворота управляемых колес по времени и характер изменения углов увода передних и задней осей автомобиля.

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81
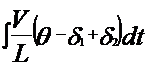