| > |
| (4.50) | ||
< |
Под временем ![]() подразумевается время непосредственного изменения траектории движения при маневре. Водитель сначала реагирует на помеху (препятствие) и осознает необходимость маневра, на что требуется определенное время. Затем водитель начинает вращать рулевое колесо, однако автомобиль еще некоторое время («время реакции автомобиля»)движется прямолинейно. Поэтому для определения
подразумевается время непосредственного изменения траектории движения при маневре. Водитель сначала реагирует на помеху (препятствие) и осознает необходимость маневра, на что требуется определенное время. Затем водитель начинает вращать рулевое колесо, однако автомобиль еще некоторое время («время реакции автомобиля»)движется прямолинейно. Поэтому для определения ![]() нужно из всего времени, за которое необходимо произвести маневр, вычесть время реагирования водителя на помеху, осознание необходимости маневра, а также время вращения рулевого колеса до момента начала изменения курсового угла. Время же, за которое водителю необходимо произвести маневр, эксперту задается следователем (судом) или может быть вычислено на основе других данных. Это может быть, например, время движения пешехода до момента наезда на него или время, за которое автомобиль преодолевает расстояние видимости.
нужно из всего времени, за которое необходимо произвести маневр, вычесть время реагирования водителя на помеху, осознание необходимости маневра, а также время вращения рулевого колеса до момента начала изменения курсового угла. Время же, за которое водителю необходимо произвести маневр, эксперту задается следователем (судом) или может быть вычислено на основе других данных. Это может быть, например, время движения пешехода до момента наезда на него или время, за которое автомобиль преодолевает расстояние видимости.
Величина времени реакции водителя на появление помехи движению и осознание необходимости маневра зависит от многих факторов. Однако, по имеющимся данным, она заметно не отличается от времени реакции при торможении автомобиля. Определение этой величины путем исследования представляется желательным. До получения же исчерпывающих данных можно в порядке первого приближения принимать значения, указанные в Методическом письме Министерства юстиции РСФСР № 000 от 27 июня 1959г., а именно от 0,4 до 1,0 с. Время реакции автомобиля также зависит от многих факторов и должно быть определено экспериментально. По имеющимся опытным данным, его значения находятся в пределах:
0,15-0,4 с – для легковых автомобилей;
0,2-0,6 с – для грузовых автомобилей и автобусов.
Если 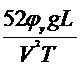 >
>![]() , то курсовой угол и траекторию движения следует рассчитывать по формулам (4.22), (4.44), (4.46) в конце маневра – по формулам (4.16), (4.48); если
, то курсовой угол и траекторию движения следует рассчитывать по формулам (4.22), (4.44), (4.46) в конце маневра – по формулам (4.16), (4.48); если 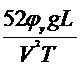 <
<![]() - по формулам (4.36), (4.45), (4.47) или (4.30), (4.49).
- по формулам (4.36), (4.45), (4.47) или (4.30), (4.49).
Пример I. произошел наезд на пешехода, который пересекая проезжую часть и двигался 5 с до наезда. Автомобиль ГАЗ-24 «Волга» двигался со скоростью 30 км/ч по мокрой асфальтированной проезжей части дороги горизонтального профиля. Необходимо установить, имел ли возможность водитель за 5 с произвести маневр так, чтобы при достижении пешеходом места наезда автомобиль уже двигался бы по другой полосе движения.
Удар по пешеходу был нанесен серединой передней части автомобиля. Будем считать, что время с момента начала реакции водителя до момента, когда управляемые колеса автомобиля начинают поворачиваться, равно 1 с, а коэффициент ![]() =
=![]() .
.
Тогда
|
Полученное значение скорости меньше значения скорости поворота управляемых колес, определенного по формуле (4.13) и равного 0,19 1/с. Поэтому конечное значение надо рассчитывать по формуле (4.49):
| (4.51) |
По формуле (4.42) определим значение ![]()
|
Подставив значения в формулу (4.51), имеем:
= 30,3∙0,944∙0,1493 ≈ 4,2 м |
Таким образом, если бы водитель начал принимать меры за 5 с до наезда на пешехода, то к моменту, когда пешеход достиг места наезда, середина заднего моста автомобиля могла двигаться на расстоянии примерно 4 м от первоначального направления движения (рис. 4.5). расстояние от правой габаритной части автомобиля до середины задней оси равно 0,9 м. Следовательно, интервал от правой части автомобиля до наезда на пешехода (места наезда) и этот момент составил около 3 м и водитель за 5 с до наезда имел техническую возможность объехать пешехода.
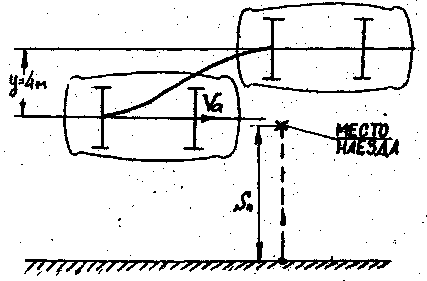
Рис. 4.5. схема предотвращения наезда на пешехода
Пример 2. Автомобиль ГАЗ-24 «Волга» двигался со скоростью 50 км/ч при видимости неподвижного неосвещенного препятствия 28 м на расстоянии 1 м от правой границы проезжей части. Препятствие было расположено у правой по ходу движения автомобиля границы проезжей части и левая габаритная его точка находилась на расстоянии 1,4 м от этой границы. Наезд на препятствие произошел без торможения. Покрытие – мокрый асфальтобетон (![]() =0,2).
=0,2).
Определим возможность объезда препятствия. Расстояние 28 м автомобиль, движущийся со скоростью 50 км/ч, преодолевает за 2 с и, если время с начала реакции водителя до момента, когда управляемые колеса начали поворачиваться, составляет 1 с, то на маневр водителю остается около 1 с.
Согласно формуле (4.50)
|
Полученное значение больше, чем скорость поворота управляемых колес, подсчитанная по формуле (4.13) и равная 0,135, поэтому конечное значение ![]() вычислим по формуле (4.47).
вычислим по формуле (4.47).
Найдем коэффициент маневра
|
Подставив значения в (4.47), получим
= 12,4∙0,981∙0,027 ≈ 0,3 м |
Следовательно, автомобиль может сместиться в поперечном направлении только на 0,3 м и наезд на препятствие неизбежен.
§ 3. Экспертное исследование других видов маневра
В экспертной практике возникают вопросы, связанные с маневрированием автомобиля, когда необходимо определить траектории движения автомобиля при поворотах на перекрестке, закругления дороги, въезде во двор и других случаях. При таких маневрах водитель, повернув рулевое колесо на задний угол, держит его неподвижным некоторое время, а затем возвращает в нейтральное положение.
Процесс движения автомобиля при таком повороте состоит из трех фаз (рис.4.6).
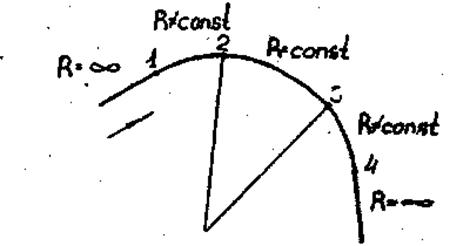
Рис. 4.6. Траектория поворота автомобиля
1. Фаза входа в поворот (участок 1-2). Водитель поворачивает передние колеса из нейтрального положения, автомобиль, двигавшийся вначале прямолинейно, движется по кривой уменьшающегося радиуса.
2. Фаза поворота с постоянным радиусом (участок 2-3). Передние колеса автомобиля повернуты на определенный угол, автомобиль движется по кривой, близкой к дуге окружности.
3. Фаза выхода из поворота (участок 3-4). Водитель возвращает колеса в нейтральное положение, автомобиль движется по дуге увеличивающегося радиуса. В конце этой фазы автомобиль снова движется прямолинейно.
Для решения вопросов о траектории движения автомобиля, временных показателей маневра, возможности «вписаться» в поворот и т. д. можно воспользоваться методикой, изложенной в работах В. А. Иларионова для автомобиля с жесткими шинами[19], внеся поправки на поперечную эластичность шин, т. е. применить коэффициент маневра ![]() (см. § 4.2). согласно методике водитель поворачивает управляемые колеса с постоянной скоростью. Радиус поворота дороги обычно известен (эти данные легко могут быть получены путем запроса следователем (судом) соответствующей дорожной организации или с помощью геодезической съемки), так же как и расположение центра поворота относительно элементов дороги. Обладая этими данными и сведениями о скорости движения автомобиля, эксперт может с помощью содержащихся в указанной методике формул решать различные вопросы, связанные с поворотом дороги, поворотом на перекрестке и т. д. Например, он может рассчитать скорость управляемых колес в начале поворота и сравнить со скоростью, вычисленной по формулам (4.9) - (4.11), или, приняв скорость управляемых колес, определенную по формулам (4.9) - (4.11), установить время, когда водителю следовало начать поворачивать управляемые колеса, а также положение, проехав, водитель уже не сможет «вписаться» в поворот постоянного радиуса.
(см. § 4.2). согласно методике водитель поворачивает управляемые колеса с постоянной скоростью. Радиус поворота дороги обычно известен (эти данные легко могут быть получены путем запроса следователем (судом) соответствующей дорожной организации или с помощью геодезической съемки), так же как и расположение центра поворота относительно элементов дороги. Обладая этими данными и сведениями о скорости движения автомобиля, эксперт может с помощью содержащихся в указанной методике формул решать различные вопросы, связанные с поворотом дороги, поворотом на перекрестке и т. д. Например, он может рассчитать скорость управляемых колес в начале поворота и сравнить со скоростью, вычисленной по формулам (4.9) - (4.11), или, приняв скорость управляемых колес, определенную по формулам (4.9) - (4.11), установить время, когда водителю следовало начать поворачивать управляемые колеса, а также положение, проехав, водитель уже не сможет «вписаться» в поворот постоянного радиуса.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 |




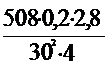 =0,08 1/с.
=0,08 1/с.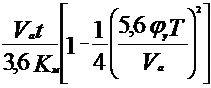
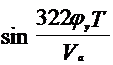 .
.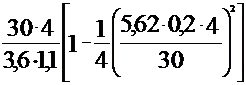
 =
=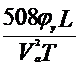 =
=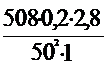 =0,138
=0,138
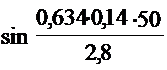 =
=