- | (4.65) |
Формулы (4.64) и (4.65) позволяют решать ряд задач, которые часто ставятся перед экспертом.
Так, если известны радиус поворота дороги (или желаемый радиус поворота автомобиля, например, на перекрестке) и курсовой угол в конце маневра (на какой угол «поворачивает» дорога), то можно установить траекторию движения автомобиля (середины его заднего моста) на всем протяжении маневрирования.
Если дорога поворачивает на угол А (угол между осевыми линиями дорог) и имеется участок постоянного радиуса ![]() , то координаты середины задней оси в конце участка 0-1 (см. рис. 4.8)определяется по формулам (4.53) и (4.54), а курсовой угол – по формуле (4.52). предложив, что угол А>90º и применив аналогичный метод вывода, получим формулы несколько другого вида.
, то координаты середины задней оси в конце участка 0-1 (см. рис. 4.8)определяется по формулам (4.53) и (4.54), а курсовой угол – по формуле (4.52). предложив, что угол А>90º и применив аналогичный метод вывода, получим формулы несколько другого вида.
В конце второго участка (в конце участка движения по постоянному радиусу) координаты ![]() и
и ![]() составят (при А>90º):
составят (при А>90º):
| (4.66) |
| (4.67) |
где ![]() и
и ![]() - координаты точки В в конце участка, м;
- координаты точки В в конце участка, м;
![]() - радиус поворота, м;
- радиус поворота, м;
![]() - курсовой угол в конце участка 0-1 и начала участка 1-2, град;
- курсовой угол в конце участка 0-1 и начала участка 1-2, град;
A - угол изменения дороги, град.
Применив метод расчета, аналогичный используемому при выведении формул (4.56) – (4.58), можно найти траекторию той же точки В автомобиля в момент выхода на прямолинейный участок дороги:
- | (4.68) |
+ | (4.69) |
В конце участка автомобиль движется под углом А к первоначальному движению.
Приведенные выражения не учитывают эластичность шин. При скоростях до 20 км/ч эластичность шин существенно не влияет на траекторию движения автомобиля, при скоростях движения более 20 км/ч следует вводить поправку на нее, для чего можно воспользоваться зависимостями (4.41) – (4.43).
Пример. На перекрестке дорог водителю автомобиля ГАЗ-24 «Волга», движущегося со скоростью 15 км/ч, нужно выполнить поворот на 90º, причем бордюрный камень на перекрестке выложен по дуге окружности радиусом 15 м. Необходимо установить, на каком расстоянии от границы проезжей части и на каком расстоянии от начала закругления водителю следует начать поворачивать управляемые колеса, чтобы заднее левое колесо прошло на расстоянии 1 м от бордюрного камня.
Середина заднего моста автомобиля должна двигаться по отрезку окружности радиусом 16,7 м (эта окружность должна быть концентричной закруглению бордюрного камня радиусом 15 м). Радиус 16,7 м – сумма 15 м, интервала (1м) и половины колеи автомобиля ГАЗ-24 (0,7м). вычислим координаты ![]() и
и ![]() по формулам (4.57) и (4.58), приняв
по формулам (4.57) и (4.58), приняв ![]() =16,7м и
=16,7м и ![]() =0,2 1/с. База автомобиля ГАЗ-24 «Волга» - 2,8м.
=0,2 1/с. База автомобиля ГАЗ-24 «Волга» - 2,8м.
|
Второе слагаемое формул (4.57) и (4.58) при принятых для расчета значениях мало и здесь не приводится.
Поперечное смещение
|
Таким образом, чтобы двигаться по дуге желаемого радиуса поворота, водителю необходимо начать поворачивать управляемые колеса, когда задние колеса находятся на расстоянии примерно 3,5 и до начала закругления бордюрного камня, т. е. когда передняя часть автомобиля примерно поравняется с началом закругления бордюрного камня. Для того чтобы заднее колесо прошло на расстоянии 1м от бордюрного камня, автомобиль до начала поворота колес должен двигаться на расстоянии около 1,2 м от границы проезжей части.
§ 4. Исследование маневра автомобиля в критических ситуациях с помощью ЭВМ
При использовании самой простой схемы автомобиля с жесткими шинами необходимо введение поправочных коэффициентов, чтобы приблизить результаты расчетов в реальному движению автомобиля. Значения этих коэффициентов определены лишь для некоторых моделей ТС, поэтому нужны дальнейшие экспериментальные исследования. Часто применяют сложные расчетные схемы, учитывающие влияние наиболее существенных факторов.
В литературе встречаются очень сложные расчетные схемы. Исследователи, прибегающие к ним, стремятся учесть как можно больше связей и соотношений и описать движение автомобиля в общем случае. Так, например, в работе коллектива авторов под редакцией А. А. Хачатурова «Динамика системы дорога – шина – автомобиль - водитель» (М., 1976) приводится расчетная схема пространственной многомассовой модели, включающей кузов и неподрессорные массы. Эта схема настолько сложна, что только шесть дифференциальных уравнений движения автомобиля, решенных относительно старших производных, содержит более 50 коэффициентов, которые сами зависят от различных параметров и условий. Практически непригодность подобных моделей очевидна.
Наиболее распространена модель, в которой автомобиль представляется в виде двухколесной тележки, причем заднее колесо (ведущее) может только вращаться, а переднее – вращаться и поворачиваться относительно вертикальной оси (управляемое колесо). Подобная расчетная схема используется в работах Я. М. Повзнера, Е. А. Чудакова, Д. Уиткома и У. Милликена и др. Движение автомобиля, представленного такой расчетной моделью, может быть описано системой уравнений[20]:

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 |




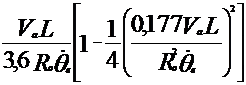
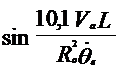 -
-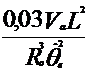

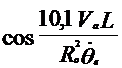 +
+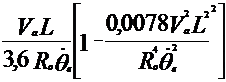
 -
-
 ;
;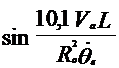 ;
;
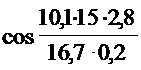 ≈ 3,45м
≈ 3,45м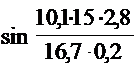 ≈ 0,4м
≈ 0,4м