Занос автомобиля может привести к опрокидыванию, если возрастает сопротивление его поперечному перемещению, например если колеса ударятся о неровность дороги или бордюр тротуара (рис. 3.7).
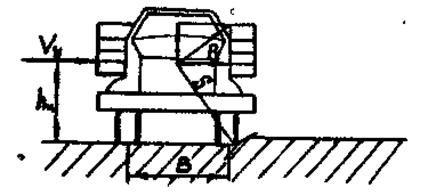
Рис. 3.7. Схема опрокидывания
При этом автомобиль может опрокинуться даже в том случае, если скорость поперечного движения ![]() его невелика. Для этого достаточно, чтобы центр тяжести автомобиля при наезде на неровность поднялся на высоту
его невелика. Для этого достаточно, чтобы центр тяжести автомобиля при наезде на неровность поднялся на высоту ![]() от поверхности дороги:
от поверхности дороги:
| (3.32) |
Согласно теореме кинетической энергии можно записать
| (3.33) |
Откуда скорость поперечного смещения
| (3.34) |
Например, при боковом заносе автомобиль ГАЗ-21 «Волга» без пассажиров достиг бордюрного камня тротуара и опрокинулся. Если не учитывать смягчающего действия шин и подвески, то боковая скорость автомобиля перед наездом на бордюрный камень могла быть около 9,5 км/ч:
|
Где колея автомобиля ГАЗ «Волга» (В) равна 1,5м, высота центра тяжести автомобиля (![]() ) 0,62 м.
) 0,62 м.
Следовательно, для опрокидывания легкового автомобиля в принятых условиях достаточно невысокой боковой скорости.
§ 4. потеря поперечной устойчивости транспортных средств на негоризонтальной дороге.
При движении автомобиля по дороге с поперечным уклоном боковой силой является составляющая массы. При криволинейном движении эта сила может складываться с центробежной силой. На рис. 3.8 показаны два автомобиля, движущиеся по криволинейному участку: автомобиль А – по внешнему краю дороги, автомобиль Б – по внутреннему1) .
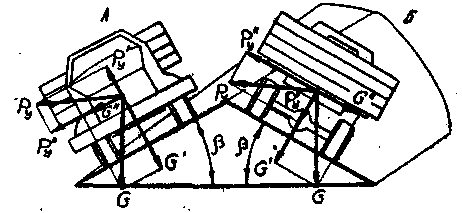
Рис. 3.8. движение автомобиля на повороте
Силу тяжести и центробежную силу у каждого автомобиля можно разложить по двум направлениям: перпендикулярно к дорожному покрытию (силы ![]() и
и![]() ) и параллельно ему (силы
) и параллельно ему (силы ![]() и
и ![]() ). У автомобиля Б силы
). У автомобиля Б силы ![]() и
и![]() действуют в противоположных направлениях частично уравновешивают друг друга, а силы
действуют в противоположных направлениях частично уравновешивают друг друга, а силы ![]() и
и![]() складываются, увеличивая силу сцепления.
складываются, увеличивая силу сцепления.
У автомобиля А, движущегося по внешнему краю дороги, силы ![]() и
и ![]() складываются, увеличивая возможность потери устойчивости, а силы
складываются, увеличивая возможность потери устойчивости, а силы ![]() и
и ![]() частично уравновешиваются, уменьшая силу сцепления.
частично уравновешиваются, уменьшая силу сцепления.
|
| (3.35) |
Для сохранения устойчивости автомобилем А должно быть соблюдено условие
| (3.36) |
Кроме того, для автомобиля с шинами, жесткими в поперечном направлении
| (3.37) |
Подставляя в (3.36) значения сил, находим величину критической скорости автомобиля по условиям заноса:
| (3.38) |
Аналогично получаем выражение для критического угла косогора:
| (3.39) |
Знак «-» в формулах (3.38) и (3.39) соответствует движению автомобиля по внешнему краю дороги на закруглении, а знак «+» - по ее внутренней стороне.
В момент начала опрокидывания автомобиля А и отрыва левых его колес от дороги вертикальные реакции на этих колесах равны нулю.
Согласно условиям равновесия
| (3.40) |
Подставив в (3.40) значения сил, можно определить критическую скорость по условиям опрокидывания:
| (3.41) |
Критический угол косогора по условиям опрокидывания
| (3.42) |
В некоторых случаях при решении экспертных задач вместо определения ![]() и
и ![]() целесообразнее подсчитать радиус, по которому может двигаться автомобиль при определенной скорости.
целесообразнее подсчитать радиус, по которому может двигаться автомобиль при определенной скорости.
Так, для движения автомобиля без заноса должно соблюдаться условие
| (3.43) |
На проезжей части без поперечного уклона
| (3.44) |
Например, при коэффициенте сцепления шин с дорогой в боковом направлении 0,4 и движении с постоянной скоростью 60 км/ч на проезжей части без бокового уклона автомобиль по условиям заноса может двигаться по дуге постоянного радиуса более 71м:

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 |




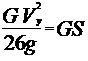 .
.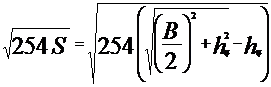 .
.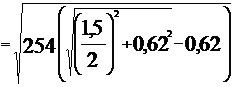
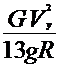 .
.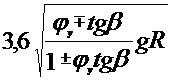 .
.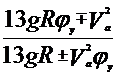 .
.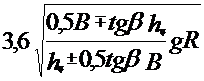 .
.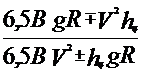 .
.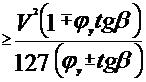 .
.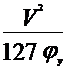 .
.