Методические рекомендации по оценке эффективности строительства, реконструкции, капитального ремонта и ремонта автомобильных дорог (стр. 25 )

; (57)

или

, , (58)

где K – количество участков дороги, на которых предусматривалось осуществление воспроизводственных мероприятий;

k – порядковый номер участка автомобильной дороги (k = 1,2, … , K);

Хk – переменная, показывающая в долях единицы степень вхождения k –го участка в план воспроизводства дороги;

F - заданный объем финансирования на простое и расширенное воспроизводство автомобильной дороги в рассматриваемом году.

Как видно из вариантов граничных условий данная задача в зависимости от транспортно-эксплуатационного состояния автомобильной дороги может решаться в двух постановках: 1) предусматривающей возможность частичного выполнения дорожных работ на каждом участке (57) и 2) не предусматривающей (58).

Реализацию моделей (55)–(58) оптимизации годовых планов осуществления стратегий воспроизводства дорожных сооружений рекомендуется осуществлять с использованием подпрограммы «Поиск решения» в среде Microsoft Excel. Рассмотрим порядок использования этой подпрограммы на следующем условном примере.

9 Пример - Допустим, что рассматривается возможность выполнения ремонта ав-

томобильной дороги в плановом году на 7 участках концентрации дорожно-транспортных происшествий в соответствии с принятой стратегией ее воспроизводства.

Требуемые объемы инвестиций на проведения ремонта К, а также показатели интегрального эффекта ЧДД от его выполнения на каждом участке дороги указаны в табл. 23.

При этом известно, что предельный объем финансирования F, который может быть направлен на реализацию данного проекта, составляет 70 млн руб.

Таблица 23 - Исходные данные для разработки стратегии воспроизводства автомобильной дороги

Поскольку величина требуемых инвестиций, как видно из табл. 23, превышает выделенный объем финансирования годового плана, возникает задача отбора в него только тех участков концентрации ДТП, проведение на которых ремонта обеспечит получение максимального совокупного интегрального эффекта.

Решение данной задачи начнем с формирования ее экономико-математической модели, которая согласно (55) и (56) может быть представлена в следующем виде

Целевая функция

17Х1 + 6Х2 + 12Х3 + 7Х4 + 2,5Х5 + 9Х6 + 7Х7 → max,

Ограничение

25Х1 + 7Х2 + 20Х3 + 10Х4 + 5Х5 + 15Х6 + 12Х7 ≤ 70.

Данная модель может реализовываться как в целочисленной постановке (при недопустимости частичного выполнения ремонтных работ на каждом участке) и в нецелочисленной.

При целочисленной постановке задачи неизвестные могут принимать значения только 0 или 1,

т. е.: Х1 = [0,1], Х2 = [0,1], Х3 = [0,1], Х4 = [0,1], Х5 = [0,1], Х4 = [0,1], Х5 = [0,1].

Рассмотрим порядок ее решения с использованием надстройки «Поиск решения».

1 Создание и заполнение формы для ввода условий задачи в операционную систему

Вид этой формы на рабочем листе Excel представлен в табл. 24. Заполнение всех ее ячеек за исключением I6 и I9 не требует особых комментариев, поскольку осуществляется путем переноса указанных в ней параметров из экономико-математической модели в соответствующую ячейку.

Что же касается ячеек I6 и I9, то в них должны быть введены не числа, а зависимости из экономико-математической модели, так как каждая из этих ячеек содержит сумму произведений неизвестных на числовые коэффициенты.

Ввод этих зависимостей осуществляется с использованием «Мастера Функций». Например, для представления целевой функции данная процедура предусматривает такую последовательность действий:

·  Курсор в I6.

·  Курсор на кнопку «Мастер функций». На экране диалоговое окно «Мастер функций» - шаг 1 из 2.

Таблица 24 - Форма для ввода в операционную систему параметров

экономико-математической модели

Примечание - ЦФ - целевая функция, ЛЧ, ПЧ - соответственно левая и правая часть ограничений.

·  Курсор в окно «Категория» на категорию «Математические». На экране Математические функции.

·  Курсор в окно «Функции» на «СУММПРОИЗВ». На экране диалоговое окно (рис. 2).

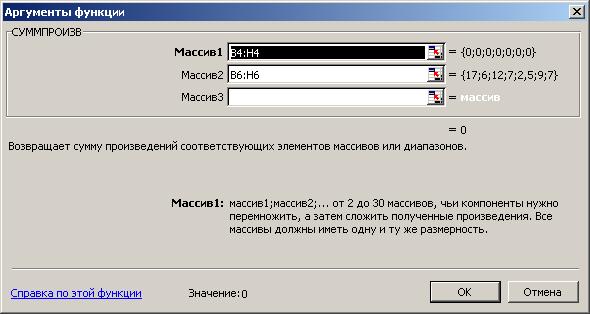
Рисунок. 2 - Диалоговое окно функции «СУММПРОИЗВ»

·  В массив 1 ввести В4:H4, а в массив 2 - В6:H6 и нажать кнопку «ОК». Поскольку в ячейках неизвестных В4:H4 не содержится никаких данных, в ячейке целевой функции I6 появится 0.

Аналогично в ячейку I9 вводится зависимость, характеризующая ограничение на размер финансирования в модели.

2 Перенос параметров модели в операционную систему и решение задачи с использованием диалогового окна «Поиск решения»

Для открытия диалогового окна «Поиск решения» (рис.3) необходимо сначала нажать на

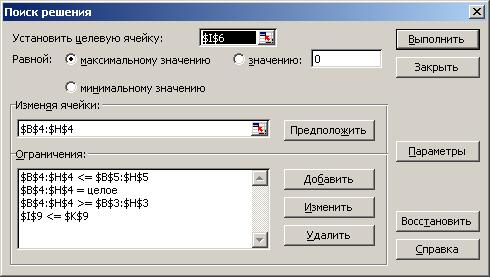
Рисунок 3 -. Диалоговое окно «Поиск решения»

кнопку «Сервис» в меню программы Excel, а затем вызвать опцию «Поиск решения».

Работа в этом окне осуществляется по следующему алгоритму.

1. Устанавливается целевая функция. Для этого курсором вводится в соответствующее окно ее адрес I6 в разработанной форме исходных данных.

2. Указывается критериальное направление целевой функции: в данном случае максимальному значению.

3. Вводятся адреса искомых переменных. Для этого курсор устанавливается в поле «Изменяя ячейки», после чего вводятся их адреса В4: H4.

4. Вводятся все ограничения модели последовательным нажатием на кнопку «Добавить».

В результате нажатия этой кнопки на экране появляется следующее окно (рис.4).

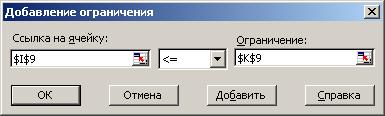
Рисунок 4 - Диалоговое окно «Добавление ограничения»

На рис. 4 показан вид окна после его заполнения ограничением на непревышение заданного объема финансирования, которое вводится в диалоговое окно «Поиск решения» нажатием кнопки «Добавить» или «ОК».

Аналогично вводятся все остальные ограничения.

5. Осуществляется решение задачи путем нажатия в диалоговом окне «Поиск решения» на кнопку «Выполнить». Если решение задачи компьютером найдено, то на экране монитора появляется следующее окно с констатацией «Решение найдено. Все ограничения и условия оптимальности выполнены» (рис. 5).

При этом результаты решения получают отображение в соответствующих ячейках разработанной формы ввода в операционную систему параметров экономико-математической модели. После решения рассматриваемой задачи она имеет следующий вид (табл. 25).

В результате решения получаем следующие значения искомых показателей:

Х 1 = Х2 = Х 3 = Х 4= Х 5 = 1; Х6 = Х7 = 0;

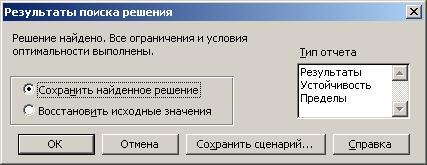
Рисунок 5 Диалоговое окно «Результаты поиска решения»

т. е. в годовой план реализации данной стратегии воспроизводства дороги входят только первый, второй, третий, четвертый и пятый участки концентрации ДТП; при этом значение целевой функции составляет 44,5 млн руб.

Таблица 25 - Вид формы для ввода в операционную систему параметров экономико-математической модели после решения задачи

6. Далее по аналогичному алгоритму осуществляем решение данной инвестиционной задачи в нецелочисленной постановке, т. е. исходя из того, что искомые Хk могут быть дробными величинами, т. е.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59