Наибольший эффект от применения методов экспертных оценок достигается при их совместном использовании с другими методами учета факторов риска, например, анализом чувствительности или методом сценариев, что может быть проиллюстрировано на следующем примере.
6 Пример - Допустим, рассматриваются три стратегии воспроизводства автомобильной дороги: вариант капитального ремонта и два варианта реконструкции: с переводом (реконструкция 1) и без перевода (реконструкция 2) дороги в более высокую техническую категорию. Величина эффекта от указанных видов воспроизводства сооружения зависит от прогнозных показателей интенсивности движения, которые устанавливаются группой экспертов на основе материалов экономических изысканий района тяготения к проектируемой дороге по оптимистическому и пессимистическому вариантам, а также от вероятности данных сценариев условий движения автотранспортных средств. Предположим, что возможность оптимистического варианта интенсивности движения по проектируемой дороге в данном случае принята экспертами с субъективной вероятностью 0,45.
Показатели интегрального эффекта по видам воспроизводства дороги по оптимистическому и пессимистическому вариантам условий движения приведены в табл. 18.
Таблица 18 - Величина интегрального эффекта от воспроизводства автомобильной дороги
Виды стратегий | Величина интегрального эффекта, (млн руб.) по вариантам движения | Ожидаемый интегральный эффект, млн руб., R | |
оптимистический (Ро = 0,45) | пессимистический (Рп = 0,55) | ||
Капитальный ремонт | 7 | 25 | 16,9 |
Реконструкция 1 | 35 | 10 | 21,25 |
Реконструкция 2 | 40 | -5 | 15,25 |
Ожидаемый интегральный эффект по каждой стратегии определяется по формуле:
R = Rо Ро + Rп Рп, (49)
где Rо, Rп - интегральный эффект соответственно при оптимистическом и пессимистическом вариантах условий движения для каждой стратегии;
Ро, Рп - вероятность соответственно оптимистического и пессимистического вариантов условий движения.
При этом очевидно, что Ро + Рп = 1 или Рп = 1 - Ро.
Тогда справедливыми являются следующие уравнения:
Rкр = 7 Ро + 25(1 - Ро) = 25 – 17 Ро ; (50)
Rр1 = 35 Ро + 10(1 - Ро) = 25 Ро + 10; (51)
Rр2 = 40 Ро - 5(1 - Ро) = 45 Ро – 5 . (52)
Приведенные в табл. 18 результаты расчета ожидаемого интегрального эффекта свидетельствуют о том, что по критерию максимальной его величины (21,25 млн. руб.) оптимальной стратегией развития дороги является ее реконструкция по первому варианту.
Однако очевидно, что в действительности фактические вероятности развития различных сценариев могут существенно отличаться от принятых экспертами субъективных вероятностей. Поэтому при оценке эффективности дорожных проектов представляет несомненный интерес определение степени чувствительности результатов от их реализации при изменении вероятностей рассматриваемых сценариев осуществления.
Для этого на основе уравнений 50 – 52 построим графики ожидаемого интегрального эффекта от вероятности оптимистического сценария условий движения (рис.1).

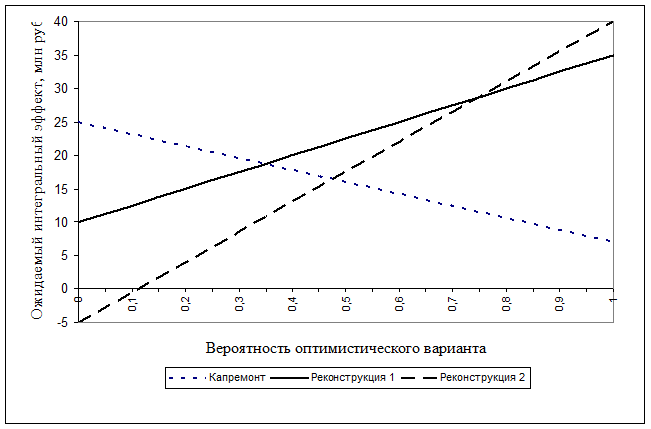
Рисунок 1 - Анализ чувствительности интегрального эффекта к изменению вероятности пессимистического варианта условий движения
Из рис. 1 видно, что при Ро = 0 ожидаемые значения интегрального эффекта соответствуют
пессимистическому сценарию условий движения, а при Ро = 1 – оптимистическому. Приведенные графики дают возможность также определить значение интегрального эффекта по каждой стратегии при любых значениях вероятности Ро и, следовательно, выбрать из них наилучшую по критерию максимума этого эффекта. Так, например, при вероятности оптимистического сценария условий движения равной 0,2 оптимальной будет стратегия капитального ремонта поскольку ожидаемый эффект при данной вероятности от ее реализации будет наибольшим (Rкр > Rр1 > Rр2).
Исходя из изложенного, на рис. 1 нетрудно выделить зоны вероятностей оптимистического сценария условий движения, при которых достигается оптимальность рассматриваемых стратегий. Так, очевидно, что при Ро от 0 до 0,35 наиболее целесообразной является стратегия капитального ремонта, при Ро от 0,35 до 0,74 - стратегия реконструкции без перевода дороги в более высокую категорию и при Ро более 0,74 – стратегия реконструкции с переводом дороги в более высокую категорию.
Метод сценариев предполагает одновременное изменение любой совокупности факторов риска и, таким образом, представляет собой комплексный анализ их влияния на результирующие показатели инвестиционных проектов. Выбор количества факторов риска, принимаемых во внимание в каждом сценарии, так же как и количество самих сценариев, зависит от особенностей проекта и степени детализации учета тех или иных факторов риска. При этом, чем больше сценариев, тем больше и вероятность получения достоверной оценки ожидаемого интегрального эффекта от реализации проекта. В настоящее время при сценарном подходе к оценке эффективности дорожных проектов, как правило, целесообразно рассматривать три основных сценария их осуществления: пессимистический, оптимистический и наиболее вероятный (реальный).
7 Пример - Для иллюстрации данного метода сформируем пессимистический, оптимистический и наиболее вероятный сценарии применительно к рассматриваемому нами дорожному проекту в Примере 1. Параметры проекта по этим сценариям с учетом ранее выявленной приоритетности факторов риска и экспертных значений вероятностей их свершения представлены в табл. 19.
Таблица 19 - Сценарии реализации дорожного проекта
Параметры проекта (факторы риска) | Вид сценария и вероятность его свершения | ||
пессимистический (Р = 0,25) | наиболее вероятный (Р = 0,50) | оптимистический (Р = 0,25) | |
Скорость движения по новой дороге, км/ч | 50 | 60 | 70 |
Капитальные вложения в строительство дороги, млн. руб. | 550 | 500 | 450 |
Начальная интенсивность движения, авт./сут | 1350 | 1450 | 1550 |
Социальная норма дисконта, % | 11 | 10 | 9 |
Доля пассажирского транспорта в потоке автомобилей | 0,6 | 0,5 | 0,4 |
Темп роста интенсивности движения, % | 2,0 | 3,0 | 4,0 |
Интегральный эффект по сценариям, млн. руб. | -202,1 | 50,9 | 395,3 |
Для выбранных сценариев величина ожидаемого интегрального эффекта от реализации дорожного проекта составит
ЧДДо = -202,1 ∙ 0,25 + 50,9 ∙ 0,5 + 395,3 ∙ 0,25 = 98,8 млн руб.
Таким образом, по результатам совокупного влияния всех факторов риска на основной показатель эффективности дорожного проекта можно сделать вывод о целесообразности его реализации.
Метод расчета предельных параметров предполагает определение таких их величин, при которых величина интегрального эффекта не выходит из зоны положительных значений. Обычно, предельные значения параметров проекта устанавливаются по сравнительно небольшой группе факторов риска (двум, трем), представляющим особую важность в тот или иной момент реализации проекта; при этом в рассмотрение принимаются наиболее неблагоприятные их сочетания.
Метод имитационного моделирования предусматривает построение вероятностной модели интегрального эффекта от определяющих его величину основных переменных параметров проекта. Модель пересчитывается при каждом новом имитационном эксперименте, в течение которого значения указанных параметров выбираются случайным образом на основе генерирования случайных чисел. Результаты всех имитационных экспериментов объединяются в выборку и анализируются с помощью статистических методов с целью получения распределения вероятностей результирующего показателя и расчета основных измерителей риска проекта.
Важную роль в отборе переменных параметров играет анализ чувствительности, осуществляющийся путем расчета рейтинга эластичности. На основании рейтинга эластичности отбираются наиболее подверженные риску переменные, т. е. колебания которых вызывают наибольшие отклонения показателей эффективности проекта.
Затем осуществляется выбор закона распределения. Если не оговорено условие вероятностной зависимости параметров, то считается, что они являются независимыми и подчиняются некоторому закону распределения. На практике чаще всего используют нормальный и равномерный законы распределения вероятностей; при этом для каждой случайной переменной задается определенный интервал с учетом наихудшего и наилучшего сценария развития события.
Основным этапом инвестиционного моделирования является процесс имитации, который выполняется следующим образом:
1. Путем компьютерной операции получения псевдослучайных чисел производится генерирование случайных чисел на заданном отрезке. Каждое новое полученное случайное число рассматривается как значение функции распределения для соответствующей переменной.
2. Значения переменных подставляются в модель, и рассчитывается интегральный показатель эффективности проекта.
3. Изложенный алгоритм повторяется заданное количество раз. Каждый имитационный эксперимент это случайный сценарий. Количество имитационных экспериментов или случайных сценариев должно быть достаточно велико (как правило, не менее 200), чтобы сделать выборку репрезентативной по отношению к бесконечному числу возможных комбинаций. Размер случайной выборки зависит от количества переменных в модели, диапазона значений переменных и требуемой точности получения результатов.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 |





