Государственный комитет Российской Федерации
ФГАОУ ”Северо - Восточный федеральный университет
им. ”
Молекулярная физика и термодинамика
Методические указания к самостоятельной работе
для студентов технических специальностей
Якутск 2011
Методическое указание к самостоятельной работе по молекулярной физике и термодинамике предназначено для студентов технических специальностей очного отделения. В каждом разделе даются основные понятия, законы и формулы, даются примеры решения типовых задач, уделяется внимание проблеме поиска решения, обоснованию выбранного способа решения, предлагаются задачи для самостоятельного решения.
Составитель:
, к. т.н., доцент кафедры теплофизики и теплоэнергетики;
Утверждено
методическим советом университета
МОЛЕКУЛЯРНОЕ СТРОЕНИЕ ВЕЩЕСТВА.
ЗАКОНЫ ИДЕАЛЬНЫХ ГАЗОВ.
Нормальные условия: 
= 0°С, 
= 101325 Па.
Идеальный газ.
Идеальный газ – это физическая модель, согласно которой:
- собственный объем молекул газа пренебрежимо мал по сравнению с объемом сосуда; между молекулами газа отсутствуют силы взаимодействия; столкновения молекул газа между собой и со стенками сосуда абсолютно упругие.
Законы, описывающие поведение идеальных газов:
1. Закон Бойля-Мариотта.
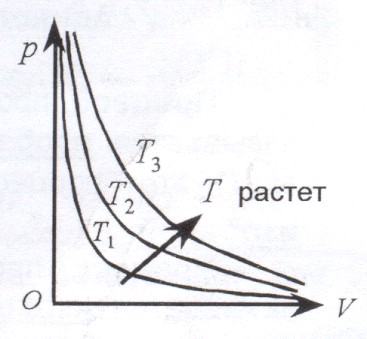
Для данной массы газа m при постоянной температуре Т произведение давления p на объем V есть величина постоянная:
при 
и 
Кривая, изображающая зависимость между p и V, характеризующая свойства вещества при постоянной температуре, называется изотермой. Изотермы – гиперболы, расположенные на графике тем выше, чем выше температура происходящего процесса.
2. Закон Авогадро.
Количество вещества 
- физическая величина, определяемая числом специфических структурных элементов – молекул, атомов или ионов, их которых состоит вещество.
Единица количества вещества - моль – количество вещества системы, содержащей столько же структурных элементов, сколько содержится в 0,012 кг изотопа углерода 12С.
В одном моле различных веществ содержится одно и то же число молекул 
, называемое числом Авогадро.
Закон Авогадро: моли любых газов при одинаковой температуре и давлении занимают одинаковые объемы.
При нормальных условиях (
, 
) этот объем 
(молярный объем) равен:
.
Молярная масса 
- это масса одного моля вещества. Отсюда: 
.
Единица молярной массы – килограмм на моль (кг/моль).
3. Закон Дальтона.
Парциальное давление – давление, которое производил бы газ, входящий в состав газовой смеси, если бы он занимал один объем, равный объему смеси при той же температуре.
Закон Дальтона: давление смеси идеальных газов равно сумме парциальных давлений 
входящих в нее газов:
или 
4. Закон Гей-Люссака.
1) Давление p данной массы m газа при постоянном объеме изменяется линейно с температурой t:
, при 
, 
.
2) Объем V данной массы m газа при постоянном давлении изменяется линейно с температурой t:
, при 
, 
,
где 
, 
и 
- объем и давление при t = 0°C.
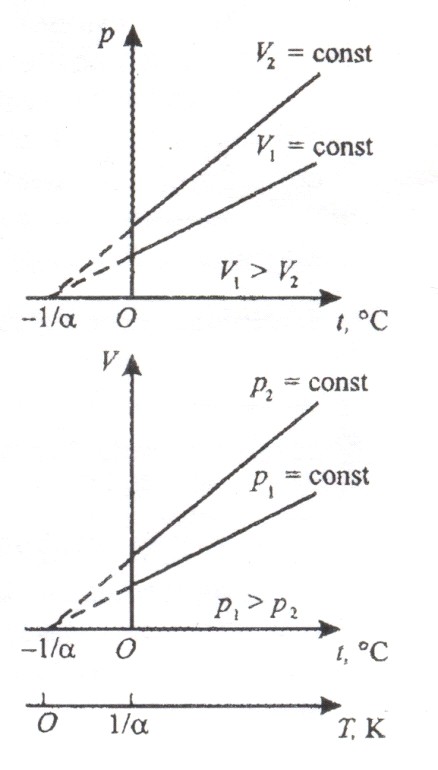
Процесс, протекающий при постоянном давлении, называется изобарным. На диаграмме в координатах (V, t) этот процесс изображается прямой, называемой изобарой.
Процесс, протекающий при постоянном объеме, называется изохорным. На диаграмме в координатах (p, t) он изображается прямой, называемой изохорой.
Изобары и изохоры пересекают ось температуры в токе 
0°C. если начало отсчета сместить в эту точку, то получим шкалу Кельвина (термодинамическую температуру): 
.
В термодинамической шкале температур:
, 
.
Откуда:
или 
при 
, 
или 
при 
, 
где индексы 1 и 2 относятся к произвольным состояниям, лежащим на одной изобаре или изохоре.
Уравнение состояния идеального газа.
* Уравнением состояния термодинамической системы называется уравнение, которое связывает давление p, объем V и температуру T термодинамической системы, находящейся в состоянии равновесия:
,
где каждая из переменных является функцией двух других.
Уравнение состояния для моля идеального газа: 
, где константа R = 8,31 Дж/(моль∙К) – называется универсальной газовой постоянной.
Объем газа массы m: 
. Отсюда 
.
Уравнение Менделеева-Клайперона – уравнение состояния для массы m идеального газа:
.
Если использовать постоянную Больцмана: 
, то уравнение состояние примет вид:
,
где 
- концентрация молекул – число молекул в единице объема.
Число молекул, содержащихся в 1 м3 газа при нормальных условиях, называется числом Лошмидта:
.
Примеры решения задач.
Пример 1. Какое количество молекул содержит единица массы водяного пара?
Решение. Число молекул, содержащееся в некоторой массе вещества, можно найти из соотношения
.
.
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
