Работа газа в адиабатическом процессе.
В адиабатическом процессе 
, поэтому 
. Если газ адиабатически расширяется от объема 
до 
, то его температура уменьшается от 
до 
и работа расширения идеального газа
.
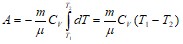Откуда получаем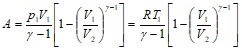 
, используя уравнение Менделеева-Клайперона 
.
Работа адиабатического расширения 1-2 (заштрихованная площадь) меньше, чем при изотермическом процессе. Это объясняется тем, что при адиабатическом расширении происходит охлаждение газа, тогда как при изотермическом расширении температура поддерживается постоянной за счет притока извне эквивалентного количества теплоты.
Политропические процессы (
).
Процесс, в котором теплоемкость остается постоянной (
) называется политропическим.
Рассмотренные выше изохорный, изотермический, изобарный и адиабатический процессы – это частные случаи политропного процесса.
Уравнение политропы
,
где коэффициент 
называется показателем политропы.
Значения теплоемкости и показателя политропы для разных процессов приведены в таблице.
Процесс | С | n |
Адиабатический |
|
|
Изотермический |
|
|
Изобарический |
|
|
Изохорный |
|
|
Теплоемкость при изотермическом процессе бесконечно велика, поскольку 
, в то время как 
. Теплоемкость при адиабатическом процессе равна нулю, поскольку 
, в то время как 
.
Задачи.
Пример 1. Определить удельные теплоемкости ср, сv для смеси 1 кг азота и 1 кг гелия.
Решение. Величина теплоемкости зависит от условий, при которых происходит нагревание газа.
Если нагревание происходит при постоянном объеме, то
,
где все сообщаемое количество теплоты идет на изменение внутренней энергии системы. Изменение внутренней энергии смеси газа определяется формулой:
.
Окончательно получим
.
Если нагревание происходит при постоянном давлении, то
,
где сообщаемое газу количество теплоты идет только на изменение внутренней энергии, но и на работу расширения газа. Работа при изобарическом расширении каждого газа равна:
; 
,
поэтому
.
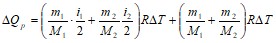Подставляя это значение, получим:
.
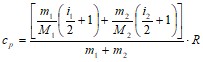Произведем вычисления:
Дж/кг⋅К,
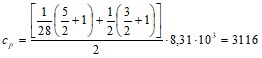Дж/кг⋅К.
Пример 2. Найти степень диссоциации кислорода б, если удельная теплоемкость при постоянном давлении равна ср=1,05 кДж (кг К).
Решение. Пусть m - полная масса кислорода. Тогда бm - масса диссоциированного кислорода, а (1-б)m-масса недиссоциированного кислорода. Количество тепла, необходимое для нагревания газа на некоторую температуру ДТ:
или 
.
Тогда 
.
Так как 
, то 
и 
.
Тогда 
;
; 
; б=0,362.
Пример 3. Газ, занимавший объем 20 л при нормальных условиях, был изобарически нагрет до 800 С. Определить работу расширения газа.
Решение. Работа расширения газа А при изобарическом процессе определяется по следующей формуле:
.
Число молей газа определим из уравнения Менделеева-Клапейрона:
, или 
.
Тогда работа будет равна:
Дж
Пример 4. Определить скорость вылета поршня массой 4 кг из цилиндра при адиабатном расширении воздуха в 40 раз, если начальное давление воздуха в 40 раз, если начальное давление воздуха 107 Па, а объем 0,3 л.
Решение. Работа А, совершаемая адиабатически расширяющимся воздухом, в данном случае идет на увеличение кинетической энергии поршня, т. е.
,
Для подсчета работа адиабатически расширяющегося газа воспользуемся формулой:
,
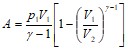Где г-отношение теплоемкостей газа при постоянном давлении и постоянном давлении и постоянном объеме (для воздуха г=1,4).
Па.
Так как 
,то 
м/с.
Пример 5. Гелий, находящийся при нормальных условиях, изотермически расширяется от объема V1=1л до объема V2=2 л. Найти работу A, совершенную газом при расширении и количество теплоты Q, сообщенное газу.
Решение. Работа, совершаемая при изотермическом изменении объема газа равна
.
Из уравнения Менделеева-Клапейрона 
.
Тогда работа будет равна:
; А=70 Дж. Согласно первому закону термодинамики 
, но т. к. Т=const, то изменение внутренней энергии равно 0, поэтому 
; Q=70 Дж.
Пример 6. Азот массой m=2 кг охлаждают при постоянном давлении от T1=400 до T2=300 К. Определить изменение внутренней энергии, внешнюю работу и количество выделенной теплоты.
Решение. Изменение внутренней энергии газа найдем по формуле:
,
СV - молярная теплоемкость. Для всех двухатомных газов
,
Тогда
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
