![]() .
.
Количество теплоты, выделяющееся при охлаждении газа при постоянном давлении:
![]() ,
,
Сp - молярная теплоемкость при постоянном давлении. Для всех двухатомных газов ![]() .
.
![]() .
.
Работа сжатия при изобарном процессе
![]() .
.
Изменение объема найдем из уравнения Менделеева-Клапейрона. При изобарном процессе: ![]() ;
;
![]() .
.
Почленным вычитанием находим :
![]() .
.
Следовательно,
![]() .
.
Подставляя числовые значения в формулы, получим:
![]() кДж.
кДж.
![]() кДж.
кДж.
![]() кДж.
кДж.
Пример 7. Аргон при давлении p=0,8 атм. Изменил объем с V1=1 л до V2=2 л. Как изменяется величина внутренней энергии, если расширение производилось при различных процессах: изобарическом, адиабатическом?
Решение. Согласно первому закону термодинамики, количество теплоты, переданное системе, может расходоваться как на увеличение внутренней энергии, так и на совершение механической работы:
![]() .
.
Величину внутренней энергии можно определить, зная массу газа, удельную теплоемкость при постоянном объеме и изменение температуры :
![]() .
.
Однако удобнее изменение внутренней энергии определять через молярную теплоемкость, которая может быть выражена через число степеней свободы:
![]() .
.
Получим: ![]() .
.
При изобарическом расширении газа согласно первому закону термодинамики часть тепла идет на изменение внутренней энергии. Определить ДU для аргона по ранее выведенной формуле нельзя, так как масса и температура газа не даны.
Используем уравнение Менделеева-Клапейрона для начального и конечного состояний газа:
![]() ;
; ![]()
или
![]() .
.
Подставим выражение в формулу
![]() .
.
Полученное уравнение является расчетным для определения ДU при изобарическом расширении.
![]() Дж.
Дж.
При адиабатическом расширении газа теплообмен со средой не происходит.
![]() .
.
Это соотношение устанавливает, что работа расширения газа может быть произведена только за счет уменьшения внутренней энергии газа.
![]() .
.
Формула работы для адиабатического процесса имеет вид:
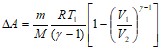 ,
,
где г - показатель степени адиабаты, который является отношением теплоемкостей:
![]() .
.
Определим изменение внутренней энергии при адиабатическом процессе для аргона:
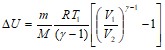 .
.
Для определения работы расширения аргона формулу следует преобразовать:
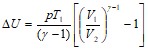 .
.
Подставляя числовые значения, получим:
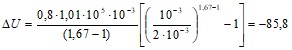 Дж.
Дж.
Пример 8. В цилиндре под поршнем находится водород, который имеет массу m=0,02 кг и начальную температуру t0=270 С. Водород сначала расширился адиабатически, увеличив свой объем в 5 раз, а затем был сжат изотермически, причем объем газа уменьшился в 5 раз. Найти температуру в конце адиабатического расширения и работу, совершенную газом.
Решение. При адиабатическом процессе температура и давление газа связаны соотношением:
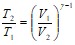 , где
, где ![]() . Для водорода г=1,4.
. Для водорода г=1,4.
Отсюда выражение для конечной температуры будет:
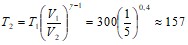 К.
К.
Работу газа при адиабатическом расширении можно определить по формуле:
![]() ,
,
![]() Дж.
Дж.
Работа газа при изотермическом процессе может быть выражена в виде:
![]() .
.
Подставляя известные числовые значения величин, входящих в правую часть равенства, находим:
![]() Дж.
Дж.
Знак «-» показывает, что при сжатии газа работа совершается над газом внешними силами. Полная работа, совершенная газом при описанных процессах, равна:
![]() Дж.
Дж.
Пример 9. Кислород массой 2 кг занимает объем V1=1 м3 и находится под давлением р1=0,2 МПа. Газ был нагрет сначала при постоянном давлении до объема V2=3 м3, а затем при постоянном объеме до давления р3=0,5 МПа. Найти изменение внутренней энергии газа, совершенную им работу и количество теплоты, переданное газу.
Решение. Изменение внутренней энергии газа выражается формулой
![]() .
.
Начальную и конечную температуру найдем, используя уравнение Менделеева-Клапейрона:
![]() .
.
Решая его относительно Т, получим
![]() .
.
![]() К ;
К ; ![]() К;
К; ![]() К.
К.
Подставляя числовые значения, получим:
![]() Дж.
Дж.
Работа расширения газа при постоянном давлении выражается формулой:
![]() .
.
Подставив числовые значения, получим
![]() Дж.
Дж.
Работа газа, нагреваемого при постоянном объеме, равна 0. Следовательно, полная работа, совершенная газом, равна
![]() Дж.
Дж.
Согласно первому началу термодинамики количество теплоты, переданное газу, равно сумме изменения внутренней энергии и работы:
![]() МДж.
МДж.
Пример 10. Идеальный двухатомный газ, находящийся в цилиндре с поршнем, первоначально занимает объем V1=4л при давлении p1=3 105 Па. Газ сначала адиабатно расширяется до объема V2=6л, а затем изохорно охлаждается. В результате давление оказывается равным p2=105 Па. Найти работу, совершенную газом; изменение его внутренней энергии; количество поглощенной теплоты.
Решение. Из условия задачи следую, что газ участвует в двух процессах.
Чтобы найти работу A и количество поглощенной теплоты ДQ при переходе из состояния 1 в состояние 2, необходимо каждый из процессов рассмотреть отдельно. При этом
![]() и
и ![]() .
.
изменение внутренней энергии не зависит от процесса и в любом случае равно
![]() .
.
Неизвестные величины можно найти из уравнения Менделеева-Клапейрона.
Адиабатный процесс протекает без теплообмена с окружающей средой.
На участке изохорного охлаждения работа газа равна АХ2=0, а количество поглощенной теплоты
![]() .
.
Используя уравнение Клапейрона-Менделеева для состояний 1 и Х, получим
![]() .
.
Уравнение адиабаты имеет вид:
![]() .
.
Для двухатомного газа 1,4. Из адиабаты следует, что
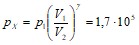 Па.
Па.
Тогда А1Х=450 Дж. Следовательно, и А12=450 Дж.
Молярная теплоемкость при постоянном объеме ![]() .
.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |





