2.87. Найти относительное число молекул, скорости которых отличаются не более чем на 1 % от значения наиболее вероятной скорости.
2.88. Какая часть молекул кислорода при 00 С обладает скоростью от 100 до 110 м/с?
2.89. Какая часть молекул азота при 1500 С обладает скоростями от 310 до 315 м/с?
2.90. Какая часть молекул водорода при 00 С обладает скоростями от 2000 до 2100 м/с?
2.91. Какая часть молекул азота, находящегося при Т=400 К, имеет скорости, лежащие в интервале от vнв до vна + Дv, где Дv= 20 м/с?
2.92. Как будет изменяться доля молекул гелия, лежащих в интервале от ‹v› до‹v›+ Дv, где Дv = 10 м/с, при увеличении температуры с 300 до 500 К? Нарисуйте графики и дайте графическое толкование решения.
2.93. Какая часть общего числа молекул имеет скорости, больше наиболее вероятной скорости и меньше наиболее вероятной скорости? Проанализируйте решение задачи.
2.94. В баллоне находится 2,5 г кислорода. Найти число молекул кислорода, скорости которых превышают значение среднеквадратичной скорости.
2.95. Найти относительное число молекул газа, скорости которых отличаются не более чем на 2 % от значения среднеквадратичной скорости.
2.96. В сосуде находится 5,0 г азота. Найти число молекул азота, скорости которых отличаются не более чем на 1 % от значения наиболее вероятной скорости.
2.97. Какова средняя квадратичная скорость атомов гелия при температуре 27°С?
2.98. При какой температуре средняя арифметическая скорость молекул водорода
1,6 км/с?
2.99. У молекул какого газа наиболее вероятная скорость при 132°С равна 460 м/с?
2.100. Найти среднюю квадратичную и среднюю арифметическую скорости молекул азота при 27° С.
2.101. Определить среднюю арифметическую скорость молекул газа, если известно, что их средняя квадратичная скорость 0,8 км/с.
2.102. Во сколько раз средняя квадратичная скорость молекул азота больше средней квадратичной скорости пылинок, взвешенных в азоте, если масса одной пылинки 10-9 г?
2.103. Сосуд емкостью 1 л содержит 1,5 г некоторого газа под давлением 2,53⋅105 Па. Определить среднюю квадратичную скорость молекул газа.
2.104. При какой температуре молекулы водорода имеют такую же среднюю квадратичную скорость, как молекулы аргона при 27° С?
ЭЛЕМЕНТЫ СТАТИСТИЧЕСКОЙ ФИЗИКИ
Барометрическая формула.
В однородном поле тяготения Земли тепловое движение молекул приводит к некоторому стационарному состоянию газа, при котором давление газа с высотой убывает. Давление на высоте h газа с молярной массой 
относительно уровня моря, где давление 
считается нормальным, равно
.
Распределение Больцмана.
Используя соотношения 
, 
, 
, получаем:
.
Так как 
- потенциальная энергия молекулы в поле тяготения, следовательно:
.
Такое распределение называют распределением Больцмана (распределение частиц по значениям потенциальной энергии) для внешнего потенциального поля.
.
Из него следует, что при постоянной температуре плотность газа больше там, где меньше потенциальная энергия его молекул.
Задачи.
Пример 1. Обсерватория расположена на высоте h=3250 м над уровнем моря. Найти давление воздуха. Температуру считать постоянной и равной t=50 С. Молярная масса воздуха равна 0,029 кг/моль. Давление воздуха на уровне моря равно p=101,3 кПа.
Решение. Закон убывания давления газа с высотой в поле силы тяжести дает барометрическая формула:
.
Подставив числовые данные, получим:
кПа.
Пример 2. На какой высоте давление воздуха составляет 75% от давления на уровне моря? Температуру воздуха считать постоянной и равной t=00 С.
Решение. Закон убывания давления газа с высотой в поле сил тяжести дает барометрическая формула:
; откуда 
.
Логарифмируя обе части уравнения, получим
, откуда 
;
м.
Пример 3. Пассажирский самолет совершает полеты на высоте h1=8300 м. Чтобы не снабжать пассажиров кислородными масками, в кабине при помощи компрессора поддерживается постоянное давление, соответствующее высоте h2=2700 м. Найти разность давлений внутри и снаружи кабины. Температура наружного воздуха считать равной t=00 С.
Решение. Согласно барометрической формуле 
, где p0=105 Па - давление на уровне моря. Тогд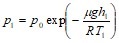а 
; 
кПа.
Температура воздуха в кабине соответствует давлению на высоте h2=2700 м, т. е. Т2=273 К, тогда
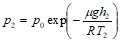; p2=71,3 кПа. Отсюда 
;
Дp = 36 кПа.
Пример 4. Найти плотность воздуха: а) у поверхности Земли; б) на высоте 4 км от поверхности Земли. Температура воздуха считать постоянной и равной 273 К. Давление воздуха у поверхности Земли 100 кПа.
Решение. а) Из уравнения Менделеева-Клапейрона 
; 
кг/м3.
б) На высоте h2=4 км плотность воздуха 
. Для нахождения p2 воспользуемся барометрической формулой
.
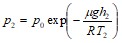Тогда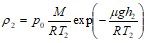 
; 
кг/м3.
Пример 5. Барометр в кабине летящего вертолета показывает давление 90 кПа. На какой высоте летит вертолет, если на взлетной площадке барометр показывает давление 100 кПа? Считать, что температура воздуха равна 290 К и не изменяется с высотой.
Решение. Распределение давления в однородном поле силы тяжести определяется барометрической формулой
.
; 
; 
;
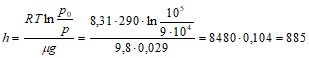м.
Пример 6. В центрифуге с ротором радиусом a=0,5 м, при температуре 300 К находится в газообразном состоянии вещество с молярной массой 1 кг/моль. Определите отношение n/n0 концентраций молекул у стенок ротора и в его центре, если ротор вращается с частотой н=30 с-1.
Решение. Распределение частиц по энергиям в силовом поле определяется законом Больцмана:
.
Сила, которая действует на молекулу массы m в центрифуге на расстоянии r от оси вращения, обусловлена перепадом давления и играет роль центростремительной силы.
Элементарная работа dA этой силы на пути dr, связана с убыванием потенциальной энергии dW, определяется так:
.
Тогда 
, а потенциальная энергия
.
При r=0, W=0, const=0.Следовательно,
.
Получим
.
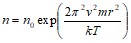При r=a получаем выражение для концентрации молекул у стенок ротора
.
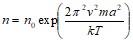Отсюда
.
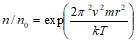Получим
.
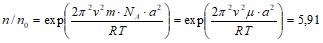Пример 7. На какой высоте плотность газа вдвое меньше плотности на уровне моря? Температуру газа читать постоянной и равной 273 К. Задачу решить для: а) воздуха, б) водорода.
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
