Молекулярная физика и термодинамика Методические указания к самостоятельной работе (стр. 14 )

       При переходе системы из одного состояния в другое изменение внутренней энергии определяется только разностью значений внутренней энергии этих состояний и не зависит от пути перехода.

Число степеней свободы.

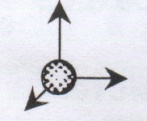
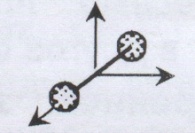
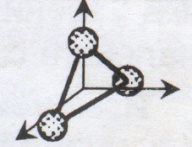
       Число степеней свободы – это число независимых переменных, полностью определяющих положение системы в пространстве.

       Число степеней свободы для идеального газа жестких молекул.

       В реальных молекулах нет жесткой связи между атомами в молекуле, поэтому необходимо учитывать также степени свободы колебательного движения атомов внутри молекулы.

       Независимо от общего числа степеней свободы молекулы, три степени свободы всегда поступательные. На каждую из них приходится треть кинетической энергии поступательного движения молекулы :

.

Закон Больцмана о равномерном распределении энергии

по степеням свободы (закон равнораспределения).

       Для системы, находящейся в состоянии термодинамического равновесия на каждую поступательную и вращательную степень свободы приходится в среднем кинетическая энергия, равная , а на каждую колебательную степень свободы – в среднем энергия, равная kT.

       Энергия колебательных степеней свободы вдвое больше, поскольку колебательная система обладает равными по величине средними значениями как кинетической, так и потенциальной энергии.

       Таким образом, средняя энергия молекулы: ,

       где i – сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы: . В классической теории рассматривают молекулы с жесткой связью между атомами; для них i совпадает с числом степеней свободы молекулы.

       В идеальном газе молекулы между собой не взаимодействуют и их потенциальная энергия равна нулю. Поэтому внутренняя энергия одного моля идеального газа и произвольной массы m газа U будут соответственно:

,  .

Теплоемкость.

       Удельная теплоемкость вещества c – величина, равная количеству теплоты, необходимому для нагревания 1 кг вещества на 1 К. Единица удельной теплоемкости – Дж/(кг∙К).

.

       Молярная теплоемкость - величина, равная количеству теплоты, необходимому для нагревания 1 моль вещества на 1 К. Единица молярной теплоемкости – Дж/(моль∙К).

.

       Связь между и с: .

       Различают теплоемкости (удельную и молярную) при постоянном объеме ( и ) и при постоянном давлении ( и ), если в процессе нагревания вещества его объем или давление поддерживаются постоянными.

Молярная теплоемкость при постоянном объеме.

       Из первого начала термодинамики , с учетом и , для 1 моль газа получим: .

       При работа внешних сил равна нулю и сообщаемая газу извне теплота идет только на увеличение его внутренней энергии.

.

        равна изменению внутренней энергии 1 моль газа при повышении его температуры на 1 К.

       Поскольку , то

.

Молярная теплоемкость при постоянном давлении.

Уравнение Майера.

       Если газ нагревается при , то

.

        не зависит от вида процесса (внутренняя энергия идеального газа не зависит ни от p, ни от V, а определяется только T) и всегда равна . Дифференцируя уравнение Клайперона-Менделеева по T при , получим

- уравнение Майера.

         всегда больше на величину универсальной газовой постоянной.

       Это объясняется тем, что при нагревании газа при постоянном давлении требуется еще дополнительное количество теплоты на совершение работы расширения газа, так как постоянство давления обеспечивается увеличением объема газа.

.

       При рассмотрении термодинамических процессов важную роль играет величина

,

которая называется коэффициентом Пуассона.

Первое начало термодинамики.

       Первое начало термодинамики – это закон сохранения и превращения энергии в термодинамических процессах.

       Изменить внутреннюю энергию системы можно двумя способами: совершая над системой работу (например, сжимая газ в цилиндре с помощью поршня) или сообщая системе теплоту (например, нагревая газ в герметичном сосуде).

       Рассмотрим замкнутую, макроскопически неподвижную систему, не находящуюся во внешних силовых полях и проанализируем с энергетической точки зрения равновесный процесс перехода системы из какого-либо первоначального состояния 1 в другое состояние 2.

Изменение внутренней энергии системы в таком процессе равно разности между количеством теплоты Q, полученным системой, и работой А, совершенной системой против внешних сил

  или  .

       Первое начало термодинамики: теплота, сообщаемая системе, расходуется на изменение ее внутренней энергии и на совершение ею работы против внешних сил.

       В дифференциальной форме:  ,

       где dU (полный дифференциал) – бесконечно малое изменение внутренней энергии системы, - элементарная работа, - бесконечно малое количество теплоты и не являются полными дифференциалами.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41