3.46. Найти выражение для кинетической энергии молекул идеального газа, импульсы которых имеют наиболее вероятною значение рв.

3.47. Во сколько раз изменится значение максимума функции f(ε) распределения молекул идеального газа по энергиям, если тем­пература Т газа увеличится в два раза? Решение пояснить графиком.

3.48. Определить, во сколько раз средняя кинетическая энергия <εп> поступательного движения молекул идеального газа отлича­ется от наиболее вероятного значения εп кинетической энергии по­ступательного движения при той же температуре.

ДЛИНА СВОБОДНОГО ПРОБЕГА И

ЧИСЛО СТОЛКНОВЕНИЙ МОЛЕКУЛ.

       Путь, который в среднем проходят молекулы между двумя последовательными столкновениями называется средней длиной свободного пробега молекул.

       Минимальное расстояние, на которое сближаются при столкновении центры двух молекул, называется эффективным диаметром молекулы d.

       Так как за 1 с молекула проходит путь, равный средней арифметической скорости , и если - среднее число столкновений, испытываемых одной молекулой газа за 1 с, то средняя длина свободного пробега

.

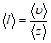       Можно показать, что: , откуда: .

       

ЯВЛЕНИЯ ПЕРЕНОСА.

  Явлениями переноса называются необратимые процессы в термодинамически неравновесных системах, в которых происходит пространственный перенос энергии (теплопроводность), массы (диффузия), импульса (внутреннее трение).

        - средняя скорость теплового движения молекул,

        - средняя длина свободного пробега.

1) Теплопроводность.

       Если в одной области газа средняя кинетическая энергия молекул больше, чем в другой, то с течением времени вследствие постоянных столкновений молекул происходит процесс выравнивания средних кинетических энергий молекул – выравнивание температур.

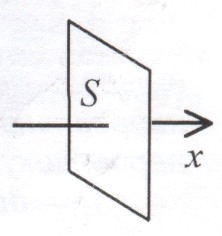
       Перенос энергии (в форме теплоты) описывается законом Фурье:

.

       Здесь - плотность теплового потока – тепловая энергия, переносимая в единицу времени через единичную площадку, перпендикулярную оси x,

,

        - коэффициент теплопроводности,

        - градиент температуры – скорость изменения температуры на единицу длины x в направлении к нормали этой площадки,

        - удельная теплоемкость газа при постоянном объеме (количество теплоты, необходимое для нагревания 1 кг газа на 1 К).

2) Диффузия.

       Явление диффузии заключается в том, что происходит самопроизвольное проникновение и перемешивание частиц двух соприкасающихся газов, жидкостей и даже твердых тел; диффузия сводится к обмену частицами (перенос масс) между этими телами, возникает и продолжается, пока существует градиент плотности.

       Перенос массы (диффузия) дли химически однородного газа подчиняется закону Фика:

.

       Здесь - плотность потока массы – масса вещества, диффундирующего в единицу времени через единичную площадку, перпендикулярную оси x,

       D – коэффициент диффузии,

,

        - градиент плотности, равный скорости изменения плотности на единицу длины x в направлении нормали к этой площадке.

3) Внутреннее трение (вязкость).

       Вследствие хаотического теплового движения молекул происходит обмен молекулами между слоями газа движущимися с различными скоростями, в результате чего импульс слоя, движущегося быстрее, уменьшается, а движущегося медленнее – увеличивается (происходит перенос импульса от одного слоя к другому). Это приводит к торможению слоя, движущегося быстрее, и ускорению слоя, движущегося медленнее.

       Внутреннее трение описывается законом Ньютона:

.

       Здесь - плотность потока импульса – полный импульс, переносимый в единицу времени в положительном направлении оси x через единичную площадку, перпендикулярную оси x.

        - динамическая вязкость,

         - градиент скорости, показывающий быстроту изменения скорости в направлении x, перпендикулярном направлению движения слоев газа.

       Внешнее сходство математических выражений, описывающих явления переноса, обусловлено общностью лежащего  основе явлений теплопроводности, диффузии и внутреннего трения молекулярного механизма перемешивания молекул в процессе их хаотического движения.

       Формулы для коэффициентов , D и связывают коэффициенты переноса и характеристики теплового движения молекул.

  Зависимости между , D и :  ,  .

Задачи.

Пример 1. В сосуде вместимостью V=0,5 л находится кислород при нормальных условиях. Найти общее число столкновений Z между молекулами кислорода в этом объеме за единицу времени. Эффективный диаметр молекулы кислорода d=0,38 нм.

Решение. Среднее число столкновений одной молекулы за единицу времени:

.

Общее число столкновений всех молекул в единице объема

.

Число столкновений молекул во всем объеме будет равно

; .

Концентрацию молекул находим из основного уравнения газового состояния:

; .

Средняя скорость молекулы.

Подставив все  параметры, получим:

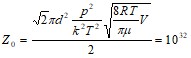1/с.

Пример 2. Сосуд емкостью V=2 л содержит азот при температуре t=270 С и давлении p=0,5 атм. Найти число молекул в сосуде, число столкновений Z между всеми молекулами за 1 с, среднюю длину свободного пробега молекул.

Решение. Число молекул в сосуде найдем исходя из уравнения Менделеева - Клапейрона:

.

В газе массой m содержится n молекул газа, так что  m=nm0,

M=m0NA.

Число столкновений каждой молекулы с остальными за 1 с:

,

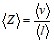Где <v>=-средняя арифметическая скорость.

Средняя длина свободного пробега молекул газа <l> определяется формулой:

,

Где d - эффективный диаметр молекулы; n0 - число молекул в единице объема.

,

Где Дж/К - постоянная Больцмана.

Поэтому для числа столкновений каждой молекулы за 1 с получим:

.

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41