При каждом соударении молекула, движущаяся перпендикулярно стенке, передает ей импульс 
. В среднем по направлению к стенке движется 
часть всех молекул. (Если рассмотреть три взаимно перпендикулярные оси, то в среднем только 
молекул движется вдоль одной из осей и только половина из них 
вдоль данного направления). Поэтому за время 
площадки 
достигнут 
молекул и передадут ей импульс 
.
Давление, оказываемее газом на стенку сосуда: 
.
Если газ в объеме V содержит N молекул, движущихся со скоростями 
, то целесообразно рассматривать среднюю квадратичную скорость, которая определяется как
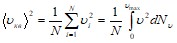
и характеризует всю совокупность молекул газа.
Основное уравнение молекулярно-кинетической теории идеальных газов:
|
.
Другие варианты записи этого уравнения с учетом соотношений 
и 
Здесь E – суммарная кинетическая энергия поступательного движения всех молекул газа, 
- молярный объем, 
- молярная масса.
Используя уравнение Клайперона-Менделеева, получим
, откуда
.
Средняя квадратичная скорость молекул идеального газа:
,
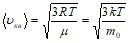где использовано 
и 
.
Средняя кинетическая энергия поступательного движения одной молекулы идеального газа:
.
Отсюда следует, что 
при 
- прекращается движение молекул газа.
Молекулярно-кинетическое толкование температуры: термодинамическая температура – есть мера средней кинетической энергии поступательного движения молекул газа.
Закон Максвелла о распределении молекул
идеального газа по скоростям.
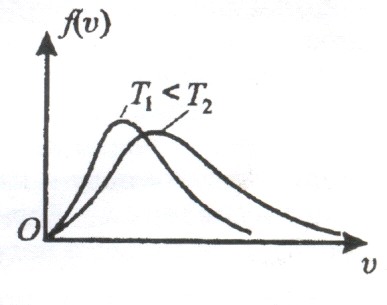
В газе, находящемся в состоянии равновесия при данной температуре, устанавливается некоторое стационарное, не меняющееся со временем распределение молекул по скоростям. Это распределение описывается функцией 
, называемой функцией распределения молекул по скоростям, которая определяет относительное число молекул, скорости которых лежат в интервале от 
до 
, т. е.
.
Закон Максвелла:
.
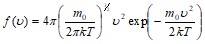Эта функция удовлетворяет условию нормировки: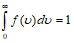 
.
Наиболее вероятная скорость молекул идеального газа.
Скорость, при которой функция распределения молекул идеального газа по скоростям максимальна, называется наиболее вероятной скоростью 
.
Приравняв 
к нулю, получаем: 
.
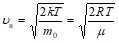С повышением температуры 
растет.
Средняя скорость молекулы газа (средняя арифметическая скорость).
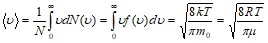
Скорости, характеризующие состояние газа.
Наиболее вероятная скорость | Средняя скорость | Средняя квадратичная скорость |
|
|
|
Примеры решения задач.
Пример 1. Найти число молекул азота в 1 м3, если давление равно p=3,69 атм., а средняя квадратичная скорость молекул равна 2400 м/с.
Решение. Основное уравнение МКТ газов имеет вид:
.
Масса одной молекулы равна
,
Получим:
,
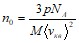м-3.
Пример 2. Найти среднюю квадратичную скорость молекул воздуха при температуре t=170 С. Молярная масса воздуха 0,029 кг/моль.
Решение. Средняя квадратичная скорость молекул равна
.
Для молекул воздуха 
м/с.
Пример 3. Во сколько раз средняя квадратичная скорость пылинки, взвешенной в воздухе, меньше средней квадратичной скорости молекул воздуха? Масса пылинки m=10-3 г. Воздух считать однородным газом, молярная масса которого М=0,029 кг/моль.
Решение. Среднюю квадратичную скорость можно выразить с помощью следующих соотношений:
.
Для пылинки 
. Для воздуха 
.
; 
.
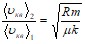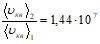Пример 4. Средняя квадратичная скорость молекул некоторого газа равна <х>=450 м/с. Давление газа p=50 кПа. Найти плотность с газа при этих условиях.
Решение. Давление газа определяется основным уравнением МКТ:
.
Кроме того n и с связаны соотношением:
.
Тогда уравнение можно записать следующим образом:
.
Откуда 
; 
кг/м3.
Пример 5. Какая часть молекул азота при температуре 1500 С обладает скоростями от 300 до 325 м/с?
Решение. Из закона Максвелла имеем 
,
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
