Решение. Из уравнения Ван-дер-Ваальса
,
, где 
;
кПа.
Давление, производимое газом на стенки сосуда, найдем из уравнения Ван-дер-Ваальса:
.
Вычисления дают следующий результат:
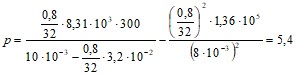МПа.
К=2,46 %.
Следовательно, давление газа, обусловленное силами притяжения молекул, составляет 2,5 % давления газа на стенки сосуда.
Пример 8. Вычислить давление водорода вблизи критического состояния для Т=35 К, если молярный объем равен 0,1 м3.
Решение. Чтобы найти давление при заданных значениях температуры и объема, решаем уравнение Ван-дер-Ваальса относительно р:
.
Вблизи критического состояния индивидуальная газовая постоянная равна 6,76 кДж/(К⋅ моль).
Па.
Давление реального газа составляет:
Па.
Пример 9. Найти изменение внутренней энергии хлора при его изотермическом расширении от V1=200 см3 до V2=500 см3, если количество хлора составляет m=20 г.
Решение. Внутренняя энергия реального газа определяется выражением
.
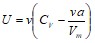Выразим неизвестные величины и подставим в формулу
; 
.
.
Изменение внутренней энергии в результате изотермического расширения найдем как разность двух значений внутренней энергии при объемах V2 и V1:
,
Тогда
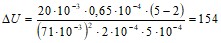Дж.
Пример 10. Как изменится высота поднятия спирта между двумя пластинками, погруженными в спирт, если расстояние между ними уменьшить с 1 мм до 0,5 мм? Смачивание пластинок считать полным.
Решение. Поверхность смачивающей жидкости между пластинами принимает цилиндрический вид.
Лапласовское давление равно:
,
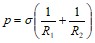где R1 и R2 – радиусы кривизны двух взаимно перпендикулярных нормальных сечений поверхности жидкости. Для цилиндрической поверхности одно из нормальных сечений – сечение, идущее вдоль образующей цилиндра. Для него R1=
. Второе, перпендикулярное ему сечение, дает окружность с радиусом R2=r/2 , где r - расстояние между плоскостями.
Поэтому добавочное давление
,
Это давление уравновешивает давление столба жидкости высотой h, поэтому
.
Отсюда
.
В нашем случае
; 
;
.
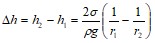Произведем вычисления:
м.
Пример 11. Из капиллярной трубки с радиусом канала r=0,2 мм по капле вытекает жидкость. Масса 100 капель равна m=0,282 г. Определить коэффициент поверхностного натяжения жидкости.
Решение. Капля отрывается в тот момент, когда ее сила тяжести равна силе поверхностного натяжения. Считая радиус шейки капли равным радиусу капилляра, можно записать 
, откуда
;
Н/м.
Пример 12. Найти добавочное давление внутри мыльного пузыря диаметром 10 см. Какую работу нужно совершить, чтобы выдуть этот пузырь?
Решение. Пленка мыльного пузыря имеет две сферические поверхности - внешнюю и внутреннюю. Обе поверхности оказывают давление на воздух, заключенный внутри пузыря. Так как толщина пленки чрезвычайно мала, то диаметры обоих поверхностей практически одинаковы. Поэтому добавочное давление
,
где r- радиус пузыря.
Так как 
, то 
.
Коэффициент поверхностного натяжения мыльной воды у=40 мН/м, диаметр пузыря 10 см. Следовательно,
Па.
Работа, которую нужно совершить, чтобы, растягивая пленку, увеличить ее поверхность на, выражается формулой:
или 
.
В данном случае S - общая площадь двух сферических поверхностей пленки мыльного пузыря, S0- общая площадь двух поверхностей плоской пленки, затягивавшей отверстие трубки до выдувания пузыря. Пренебрегая этой величиной, получим:
.
Сделав подстановку числовых значений величин. Получим:
Дж.
Пример 13. Глицерин поднялся в капиллярной трубке на высоту h=25 мм. Определить коэффициент поверхностного натяжения глицерина, если диаметр канала трубки d=0,8 мм, а плотность глицерина с=1,26⋅103 кг/м3.
Решение. Высота поднятия жидкости в цилиндрическом капилляре радиуса a равна:
.
Радиус капилляра и угол связаны соотношением
,
где R-радиус мениска.
Принимая 
, получим R=d/2
Н/м.
Уравнение Ван-дер-Ваальса.
5.1. В сосуде вместимостью V=10 л находится азот массой m=0,25 кг. Определить: 1) внутреннее давление р' газа: 2) собственный объем V′ молекул.
5.2. Определить давление р, которое будет производить кислород, содержащий количество вещества ν=l моль, если он занимает объём V=0,5 л при температуре T=300 К. Сравнить полученный результат с давлением, вычисленным по уравнению Менделеева — Клапейрона.
5.3. В сосуде вместимостью V=0,3 л находится углекислый газ, содержащий количество вещества ν=l моль при температуре Т=300 К. Определить давление р газа: 1) по уравнению Менделеева — Клапейрона; 2) по уравнению Ван-дер-Ваальса.
5.4. Криптон, содержащий количество вещества ν=l моль, находится при температуре T=300 К. Определить относительную погрешность ε=Δp/p, которая будет допущена при вычислении давления, если вместо уравнения Ван-дер-Ваальса воспользоваться уравнением Менделеева — Клапейрона. Вычисления выполнить для двух значений объема: 1) V=2 л; 2) V=0,2 л.
5.5. Внутреннюю полость толстостенного стального баллона наполовину заполнили водой при комнатной температуре. После этого баллон герметически закупорили и нагрели до температуры T=650 К. Определить давление р водяного пара в баллоне при этой температуре.
5.6. Давление р кислорода равно 7 МПа, его плотность р=100 кг/м3. Найти температуру Т кислорода.
5.7. Определить давление р водяного пара массой m=1 кг, взятого при температуре Т=380 К и объеме V: 1) 1000 л; 2) 10 л; 3) 2 л.
5.8. Определить давление ван-дер-ваальсовского водорода при температуре t=00 С, если молярный объем равен 0,5 м3.
5.9. Определите давление p ван-дер-ваальсовского кислорода при температуре -1000 С, если молярный объем Vm равен 1л.
5.10. Определить собственный объем молекул углекислого газа, находящегося в баллоне при температуре T=00 С, если его масса m=0,5 кг.
5.11. Определить собственный объем молекул гелия, находящегося при температуре -1000 С, если его масса m=0,1 кг.
5.12. Определить собственный объем молекул гелия и собственный объем молекул хлористого водорода, если их масса одинакова и равна 0,2 кг.
5.13. Определить внутреннее давление кислорода, находящегося в баллоне вместимостью 1л при температуре 00 С. Масса кислорода m=1 кг.
5.14. Определить внутреннее давление азота, находящегося в баллоне вместимостью 1 л при температуре 00 С. Масса кислорода 0,1 кг. Сравнить полученную величину с давлением на стенки баллона.
5.15. В баллоне вместимостью V=6 л находится кислород m=0,6 кг при температуре 290 К. Найти давление газа на стенки сосуда (b=0,032 м3/(К⋅моль);a=1,36⋅105 Н⋅м4/(К⋅моль2)).
5.16. Определить давление Р водяного пара массой m=1 кг, при температуре Т=380 К в объеме 1000 и 2 л.
5.17. В сосуде вместимостью V=0,3 л находится один моль углекислого газа при температуре 300 К. Определить давление Р газа:
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
