Дело в том, что внутренняя энергия системы является однозначной функцией состояния системы. Отсюда следует, что при совершении системой произвольного процесса, в результате которого она вновь возвращается в исходное состояние, полное изменение внутренней энергии системы равно нулю (). Ни работа, ни теплота не являются функциями состояния системы.

       Все величины, входящие в первое начало термодинамики могут быть как положительными, так и отрицательными.

       Если к системе подводится теплота то > 0; если от системы отводится теплота, то < 0.

       Если система совершает работу над внешними телами, то > 0, если же над системой внешние силы совершают работу, то < 0.

       Другая формулировка первого начала термодинамики связана с тем, что если система периодически возвращается в первоначальное состояние, и, следовательно , то A = Q, т. е. вечный двигатель первого рода – периодически действующих двигатель, который совершал бы бульшую работу, чем сообщенная ему извне энергия – невозможен.

Работа газа при его расширении.

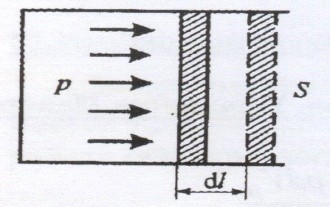
       Если находящийся под поршнем в цилиндрическом сосуде, газ, расширяясь, передвигает поршень на расстояние dl, то производит над ним работу , где S – площадь поршня.

       Полная работа A, совершаемая газом при изменении его объема от до :

.

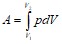       Равновесные процессы – это процессы, состоящие из последовательности равновесных состояний. Они протекают так, что изменение термодинамических параметров за конечный промежуток времени бесконечно мало. Все реальные процессы неравновесны, но в ряде случаев (достаточно медленные процессы) неравновесностью реальных процессов модно пренебречь.

       Равновесные процессы можно изображать графически в координатах (p, V). Так как работа определяется площадью заштрихованной полоски, а полная работа – площадью кривой между и .

       При неравновесных процессах значения параметров в разных частях системы различны и не существует (p, V)-точек, характеризующих состояние всей системы. Поэтому графическое изображение неравновесного процесса невозможно.

ИЗОПРОЦЕССЫ.

Рассмотрим равновесные процессы, происходящие с термодинамическими системами, при которых один из основных параметров состояния сохраняется постоянным.

Изохорный процесс ().

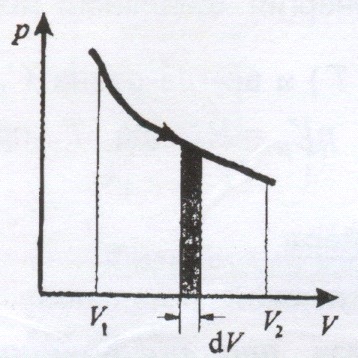
       Диаграмма этого процесса – изохора – в координатах (p, V) изображается прямой,

параллельной оси ординат (ось p). Процесс 2-1 – изохорный нагрев, процесс 2-3 – изохорное охлаждение.

       При изохорном процессе газ не совершает работу над внешними телами () и вся теплота, сообщаемая газу, идет на увеличение его внутренней энергии (). Поскольку , то для произвольной массы газа:

.

Изобарный процесс (p=const).

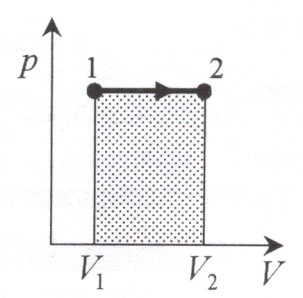
       Диаграмма этого процесса – изобара – в координатах (p, V) изображается прямо параллельной оси абсцисс (ось V). При изобарном процессе работа газа при увеличении объема от до равна:

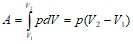
и определяется площадью заштрихованного прямоугольника. Используя уравнение Клайперона , получаем , отсюда

.

       Физический смысл универсальной газовой постоянной: К численно равна работе изобарного расширения 1 моля идеального газа при нагревании его на 1 К.

Изотермический процесс ().

       Диаграмма этого процесса – изотерма – в координатах (p, V) представляет собой

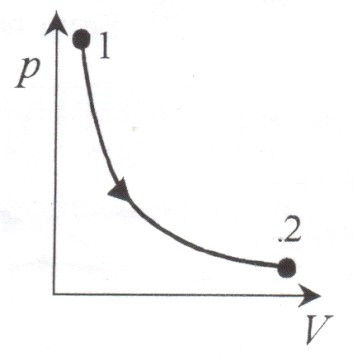
гиперболу. Изотермический процесс описывается законом Бойля-Мариотта ().

       Работа изотермического расширения газа:

.

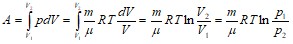       Так как при внутренняя энергия идеального газа не изменяется, то из первого начала термодинамики следует, что , то есть все количество теплоты, сообщаемое газу, расходуется на совершение им работы против внешних сил.

       Поэтому, для того, чтобы при расширении газа температура не понижалась, к газу в течение изотермического процесса необходимо подводить количество теплоты, эквивалентное внешней работе расширения.

Адиабатический процесс ().

       Адиабатическим называется процесс, при котором отсутствует теплообмен между системой и окружающей средой ().

       К адиабатическим процессам можно отнести все быстропротекающие процессы (теплообмен не успевает совершиться), например, распространение звука в среде, циклы расширения и сжатия в двигателях внутреннего сгорания, в холодильных установках и т. д.

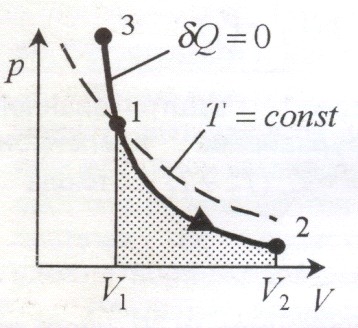
       Из первого начала термодинамики следует, что при адиабатическом процессе . Используя и , получим   (1). С другой стороны, из следует   (2). Разделив (2) на (1) получим:

  или  ,

       где - коэффициент Пуассона. Интегрирование этого уравнения дает  , откуда следует уравнение Пуассона – уравнение адиабатического процесса.

       Используя уравнение Менделеева-Клайперона , получаем:

,  .

       Диаграмма адиабатического процесса – адиабата – в координатах (p, V) изображается гиперболой. Адиабата () более крута, чем изотерма (). Это объясняется тем, что при адиабатическом сжатии 1-3 увеличение давления газа обусловлено не только уменьшением его объема, но и повышением температуры.

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41