Общее число столкновений за 1 с равно:
.
Имеем: 
.
Длина свободного пробега: 
.
Производим вычисления в СИ:
молекул,
с-1.
м.
Пример 3. При каком давлении средняя длина свободного пробега молекул водорода <l>=2,5 см при температуре 680 С? Диаметр молекул водорода принять равным d=0,23 нм.
Решение. Давление водорода при температуре Т можно найти по уравнению Менделеева-Клапейрона, в котором удобно ввести число молекул n в 1 м3. Это проводится следующим образом:
; 
,
.
Число молекул в 1 м3 выразим через длину свободного пробега. Из формулы
находим 
.
Таким образом,
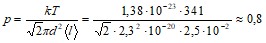Па.
Пример 4. Определить длину свободного пробега молекул и число соударений за 1 с, происходящих между всеми молекулами кислорода, находящегося в сосуде емкостью 2 л при температуре 270 С и давлении 100 кПа.
Решение. Средняя длина свободного пробега молекулы вычисляется по формуле:
,
,
Получим:
.
Число соударений, происходящих между всеми молекулами за 1 с, равно:
,
Где N-число молекул кислорода в сосуде объемом 2 л, <Z>- среднее число соударений одной молекулы за 1 с. Число молекул в сосуде:
,
Среднее число соударений молекулы за 1 с равно
,
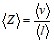Средняя арифметическая скорость молекулы равна
<х>=
.
Находим:
.
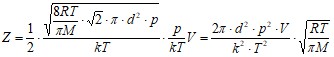Произведем вычисления:
с-1.
м.
Пример 5. Найти плотность азота, если молекула за 1 с испытывает 2,05⋅108 с-1 столкновений при температуре 280 К. Какова средняя длина свободного пробега молекул?
Решение. Плотность азота определяется по формуле
,
Массу азота можно выразить через число молекул в данном объеме и массу одной молекулы:
.
Массу одной молекулы можно найти делением массы одного моля на число Авогадро:
.
Число молекул, содержащихся в газе некоторого объема равно:
,
Имеем: 
;
Далее получим
.
Концентрацию молекул находим из формулы для числа столкновений:
, откуда
,
,
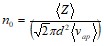Подставляя величину скорости, получим:
,
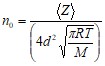Имеем: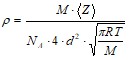 
.
Среднюю длину свободного пробега молекул азота находим по формуле:
; 
.
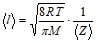Произведем вычисления:
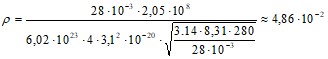кг/м3.
мкм.
Пример 6. Определить плотность с разреженного азота, если средняя длина свободного пробега молекул равна 10 см. Какова концентрация молекул?
Решение. Средняя длина свободного пробега молекул определяется формулой:
,
Где d –эффективный диаметр молекул ( для азота 0,31 нм).
Концентрацию молекул определим из равенства:
,
Решая совместно уравнения, находим:
; 
;
м.
кг/м3.
Пример 7. Какое предельное число молекул газа должно находиться в единице объема сферического сосуда, чтобы молекулы газа не сталкивались друг с другом? Эффективный диаметр молекул газа d=0,3 нм, а диаметр сосуда D=15 см.
Решение. Молекулы газа будут сталкиваться друг с другом, когда длина свободного
пробега больше или равна диаметру сосуда. Выразим длину свободного пробега
.
Отсюда
1/м3.
Пример 8. Определить коэффициент внутреннего трения для водорода, имеющего температуру t=270 С.
Решение. Из МКТ газов коэффициент внутреннего трения равен:
,
Плотность из уравнения Менделеева-Клапейрона равна:
,
Средняя арифметическая скорость молекул равна: 
,
Средняя длина свободного пробега равна: 
,
Давление и температура газа связаны соотношением:
,
откуда 
, а 
,
Получим: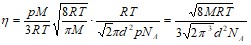 
,
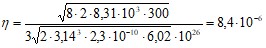кг/(м⋅с).
Пример 9. Вычислить коэффициент внутреннего трения и коэффициент диффузии кислорода, находящегося при давлении p=0,2 МПа и температуре T=280 К.
Решение. На основании представлений МКТ газов коэффициент внутреннего трения идеального газа и коэффициент диффузии определяется по формулам:
;
,
Из этого следует, что
.
Среднюю арифметическую скорость и среднюю длину свободного пробега находим по формулам:
; 
,
Из основного уравнения МКТ газов определяем n0:
,
Получим: 
.
Окончательный вид расчетной формулы для коэффициента диффузии :
.
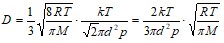Плотность кислорода определяется по формуле :
;
.
Расчетная формула для внутреннего трения:
.
Вычисляем:
м2/с.
кг/(м⋅с)
Пример 10. Найти теплопроводность водорода л, вязкость которого з=8,6 мкПа⋅с.
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
