![]() .
.
Подставив сюда найденное значение КПД и температуру нагревателя, получим:
![]() К.
К.
Пример 4. Кислород массой m=1 кг совершает цикл Карно. При изотермическом расширении газа его объем увеличился в 2 раза, а при последующем адиабатическом расширении совершается работа 3000 Дж. Определить работу, совершенную за цикл.
Решение. Идеальный цикл Карно состоит из двух изотерм и двух адиабат.
При изотермическом расширении внутренняя энергия идеального газа остается постоянной, следовательно, все подводимое тепло идет на работу расширения газа
![]() .
.
При изотермическом сжатии тепло отдается холодильнику, и это количество теплоты определяется работой, затраченной на сжатие газа:
![]() .
.
Состояния 2 и 3 лежат на одной адиабате, поэтому можно написать:
![]() .
.
Для состояний 4 и 1, которые отвечают одной адиабате, имеем:
![]() .
.
Получим
![]() .
.
Работа при адиабатическом расширении на участке 2-3 равна:
![]() .
.
Работа при адиабатическом сжатии на участке 4-1 равна:
![]() .
.
Так как Т1=Т2, а Т3=Т4, то А23=-А41, т. е. полная работа по адиабатическому сжатию и расширению равна 0.
Следовательно, работа цикла:
![]() .
.
![]() .
.
Выразим разность температур, равную Т1-Т3 и подставим в уравнение:
![]() .
.
Произведем вычисления:
![]() Дж.
Дж.
Пример 5. Тепловая машина работает по циклу Карно. При изотермическом расширении двухатомного газа его объем увеличился в 2 раза, а при последующем адиабатическом расширении - в 5 раз. Определить КПД цикла. Какую работу совершает 1 кмоль газа за один цикл, если температура нагреваК? Какое количество теплоты получит от холодильника машина, если она будет совершать тот же цикл в обратном направлении, и какое количество теплоты будет передано нагревателю?
Решение. КПД цикла Карно определяется формулой:
![]() .
.
При адиабатическом процессе 2-3:
![]() ,
,
где г - показатель адиабаты (для двухатомного газа равен 1,4).
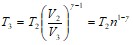 .
.
Так как Т1=Т2 , то получаем
![]() ,
,
где n1-г=51-1,4=0,525.
Следовательно, з=1-0,525=0,475.
Работа в цикле Карно определяется разностью количества теплоты Q1, полученного в процессе 1-2 и Q2, отданного в процессе 3-4:
![]() .
.
При изотермическом процессе
![]() ,
, ![]() ,
,
Так как ![]() . Знак минус показывает, что теплота отдается холодильнику.
. Знак минус показывает, что теплота отдается холодильнику.
Следовательно,
![]() ,
,
где ![]() ,
,
ДТ=300⋅0,475=142,5 К; тогда Т3=157,5 К.
Подставим числовые значения:
![]() МДж.
МДж.
При обратном цикле Карно газ расширяется по адиабате 1-4, затем изотерме 4-3, получая при этом от холодильника количество теплоты Q2; далее газ сжимается по адиабате 3-2, затем по изотерме 2-1, отдавая при этом количество теплоты Q1.
![]() МДж;
МДж;
![]() МДж.
МДж.
Пример 6. При давлении p=105 Па 0,2 моля двухатомного газа занимает объем V1=10 л. Газ изобарно сжимают до объема V2=4 л, затем сжимают адиабатно, после чего газ изотермически расширяется до начального объема и давления. Найти работу, совершенную газом за один цикл, температуру, давление, объем в характерных точках процесса, количество теплоты, полученное газом от нагревателя и отданное газом холодильнику, термический КПД цикла.
Решение. Из уравнения Менделеева-Клапейрона находим Т1:
![]() К.
К.
Из уравнения изобарного процесса ![]() находим
находим
![]() ;
; ![]() К.
К.
Найдем координаты точки пересечения адиабаты и изотермы. Из уравнения адиабатного процесса ![]() (г=1,4 для двухатомного газа), откуда
(г=1,4 для двухатомного газа), откуда
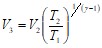 ,
,
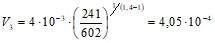 м3.
м3.
Из уравнения изотермического процесса ![]() ,
,
![]() ,
,
![]() Па.
Па.
Количество теплоты, полученное газом от нагревателя, определим по первому закону термодинамики:
![]() . При изотермическом процессе
. При изотермическом процессе ![]() и
и ![]() , следовательно,
, следовательно,
![]() кДж.
кДж.
Количество теплоты, отданное газом холодильнику при изобарном процессе, равно:
![]() .
.
Для двухатомного газа ![]() . Тогда
. Тогда
![]() кДж.
кДж.
Работа, совершенная газом,
![]() кДж.
кДж.
Находим КПД цикла:
![]() %.
%.
Пример 7. Найти КПД идеальной паровой машины, цикл работы. Паровая машина расходует за один цикл m=1 г топлива с удельной теплотой сгорания q=15,4 МДж/кг. Начальный объем V0=0,2 л, V1=1,2 л, V2=2,4 л. Начальное давление равно атмосферному, давление пара в котле p1=1 МПа, показатель адиабаты г=1,3.
Решение. Коэффициент полезного действия тепловой машины
![]() .
.
Найдем работу
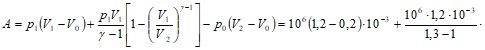
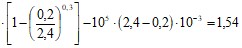 кДж.
кДж.
Тогда КПД равен
![]() .
.
Пример 8. В результате изотермического расширения объем 8 г кислорода увеличился в 2 раза. Определить изменение энтропии газа.
Решение. Изменение энтропии системы определяется по формуле
![]() .
.
При изотермическом расширении все подводимое количество теплоты идет на работу по расширению газа, т. е. ![]() .
.
Из уравнения Менделеева-Клапейрона: ![]() ,
,
поэтому
![]() .
.
Получим: 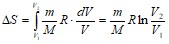 .
.
Произведем вычисления:
![]() Дж/К.
Дж/К.
Пример 9. Как изменится энтропия 2 г водорода, занимающего объем 40 л при температуре 270 К, если давление увеличить вдвое при постоянной температуре и затем повысить температуру до 320 К?
Решение. Изменение энтропии определяется формулой
![]() .
.
Изменение количества теплоты находим из первого закона термодинамики:
![]() .
.
Величину р найдем из уравнения Менделеева-Клапейрона:
![]() .
.
Для двухатомного газа ![]() .
.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |





