Тройная точка воды соответствует температуре 273,16 К (или 0,01 °С по шкале Цельсия) и является основной реперной точкой для построения термодинамической температурной шкалы.
Уравнение Клайперона-Клаузиуса.
Уравнение Клайперона-Клаузиуса 
позволяет определить.
Здесь L - (например, в случае плавления – удельная теплота плавления), 
- изменение объема вещества при переходе его из первой фазы во вторую, T – температура перехода (например, в случае плавления – температура плавления 
).
Поскольку L и T всегда положительны, то наклон кривой равновесия определяется знаком 
. Так при испарении и сублимации объем всегда возрастает, поэтому 
, т. е. увеличение давления приводит к повышению температуры плавления (сплошная КП на рисунке).
Для некоторых веществ (вода, Ge, чугун) объем жидкой фазы меньше объема твердой фазы, т. е. 
; следовательно, увеличение давления сопровождается понижением температуры плавления (штриховая линия на рисунке).
Анализ диаграммы состояния.
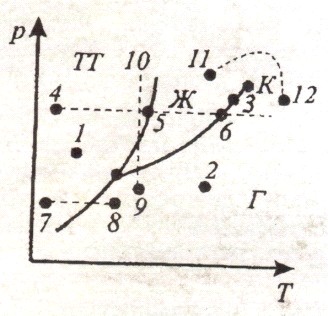
Диаграмма состояния позволяет судить, в каком состоянии находится данное вещество при определенных p и T, а также какие фазовые переходы будут происходить в том или ином процессе.
Например, при условиях, обозначенных точкой 1 вещество – в твердом состоянии (ТТ), 2 – в газообразном (Г), 3 – одновременно в жидком (Ж) и газообразном.
При изобарном нагреве 4-5-6 в точке 5 начинается плавление, 6 – кипение.
При изобарном нагреве 7-8 твердое тело превращается в газ, минуя жидкую фазу.
При изотермическом сжатии 9-10 вещество пройдет три состояния: газ-жидкость-кристалл.
Кривая испарения заканчивается критической точкой (К). Поэтому возможен непрерывный переход вещества из жидкого состояния в газообразное и обратно в обход критической точки, без пересечения кривой испарения (переход 11-12), т. е. такой переход, который не сопровождается фазовыми превращениями.
Это возможно потому, что различие между газом и жидкостью является чисто количественным (оба эти состояния, например, являются изотропными).
Переход же кристаллического состояния в жидкое или газообразное может быть только скачкообразным (в результате фазового перехода), поэтому кривые плавления и сублимации не могут обрываться, как это имеет место для кривой испарения в критической точке.
Кривая плавления уходит в бесконечность, а кривая сублимации идет в точку, где p = 0 и T = 0.
Задачи.
Пример 1. В сосуде емкостью 10 л находится 360 г водяного пара при температуре 470 К. Вычислить давление пара на стенки сосуда. Какую часть объема V составляет объем V’ молекул пара? Какую часть давления p составляет внутреннее давление p'?
Решение. По уравнению Ван-дер-Ваальса
,
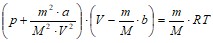где 
моль, a и b – постоянные Ван-дер-Ваальса ( для водяного пара 
и 
).
Собственный объем V’ молекул связан с поправкой b равенством
.
Тогда 
;
; 
%.
Внутреннее давление определяется равенством
;
Па.
Далее p находим из уравнения:
;
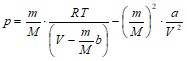Па.
; 
%.
Пример 2. Даны постоянные a и b, входящие в уравнение Ван-дер-Ваальса. Определить значение критической температуры и критического давления аргона.
Решение. Уравнение состояния реальных газов Ван-дер-Ваальса для 1 кмоля имеет вид:
.
Из уравнения можно получить выражение для критических величин:
;
.
Определяем Tк и pк:
К;
Па.
Пример 3. Углекислый газ массой m=88 г находится в сосуде емкостью V=10 л. Определить внутреннее давление газа и собственный объем молекул.
Решение. По уравнению Ван-дер-Ваальса выражение добавочного давления p’ имеет вид
.
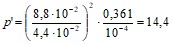кПа.
Постоянная Ван-дер-Ваальса b учитывает поправку на собственный объем молекул V’ , и, как следует из уравнения Ван-дер-Ваальса, произведение 
равно учетверенному объему молекул 
, откуда
л.
Пример 4. В сосуде емкостью V=25 л при температуре T=300 К находится 40 моль кислорода. Определить давление газа, считая его идеальным; реальным.
Решение. Давление идеального газа определяем из уравнения Менделеева-Клапейрона:
; 
Па.
Давление газа, считая его реальным, определим из уравнения Ван-дер-Ваальса:
,
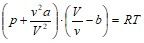Преобразуя это выражение, получим:
;
Па.
Пример 5. В сосуде под давлением p=8 МПа содержится кислород, плотность которого с=100 кг/м3. Считая газ реальным, определить его температуру и сравнить ее с температурой идеального газа при тех же условиях.
Решение. Температуру идеального газа найдем из уравнения состояния идеального газа - уравнения Менделеева-Клапейрона:
;
;
,
откуда
;
К.
Уравнение состояния реального газа - уравнение Ван-дер-Ваальса для произвольного количества газа имеет вид:
.
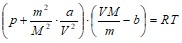Преобразуем уравнение с учетом 
.
.
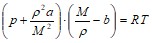Отсюда
;
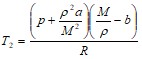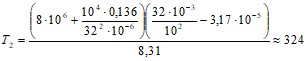К.
Пример 6. В баллоне вместимостью 8 л находится кислород массой m=0,3 кг. Найти, какую часть вместимости сосуда составляет собственный объем молекул газа (a=1,36 атм6/кмоль2; b=0,032 м3/кмоль).
Решение. Необходимо найти соотношение
.
Собственный объем молекул определим, зная, что постоянная b Ван-дер-Ваальса равна учетверенному объему молекул, содержащихся в одном моле реального газа, т. е. нb=4V.
или 
.
Таким образом
.
Пример 7. В баллоне вместимостью V=10 л находится кислород массой m=0,8 кг при температуре T=300 К. Определить давление реального газа p, внутреннее давление p’ и отношение p’/p.
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
