Тогда при m = 1, для водяного пара
![]() молекул.
молекул.
Пример 2. Какое число молекул содержит единица объема сосуда при температуре t=100 С и давлении p=1,33⋅10-9 Па?
Решение. Число молекул, содержащееся во всем сосуде, можно найти из соотношения:
![]() . Тогда число молекул в единице объема
. Тогда число молекул в единице объема ![]() . Согласно уравнению Менделеева-Клапейрона
. Согласно уравнению Менделеева-Клапейрона
![]() , откуда
, откуда ![]() .
.
Тогда ![]() ;
;![]() м-3.
м-3.
Пример 3. В сосуде вместимостью 10 л находятся m=4 г гелия при температуре t=170 С. Найти давление гелия.
Решение. По уравнению Менделееева-Клапейрона имеем:
![]() ,
, ![]() .
.
Произведем вычисления: ![]() Н/м2.
Н/м2.
Пример 4. Найти массу киломоля смеси m1=10 г угарного газа и m2=40 г кислорода
Решение. ![]() ;
;![]() . Масса смеси равна сумме масс компонент смеси
. Масса смеси равна сумме масс компонент смеси
![]() .
.
Число компонент смеси также выражается через сумму киломолей отдельных газов:
![]() ;
;
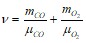 .
.
В итоге получим расчетную формулу:
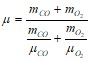 .
.
Подставим числовые значения и определим молекулярный вес данной смеси:
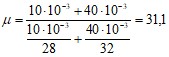 кг/ моль.
кг/ моль.
Пример 5. В баллоне находилось 8 кг газа при давлении p1=106 Па. Найти, какое количество газа взяли из баллона, если окончательное давление стало равно p2=2,5⋅105 Па. Температуру газа считать постоянной.
Решение. Количество газа определим из уравнения Клапейрона-Менделеева
![]() ;
;![]() .
.
![]() .
.
Неизвестный сомножитель в скобках найдем из уравнения Клапейрона-Меделеева:
![]() .
.
Окончательно получим:
![]() кг.
кг.
Пример 6. В сосуде объемом V=0,5 л находится масса m=1 г парообразного йода. При температуре t=10000 С давление в сосуде pc=93,3 кПа. Найти степень диссоциации б молекул йода на атомы. Молярная масса молекул йода M=0,254 кг/м3.
Решение. Степенью диссоциации называется отношение числа молекул, распавшихся на атомы, к общему числу молекул. В результате диссоциации имеем
![]() атомарного йода и
атомарного йода и ![]() молекулярного йода.
молекулярного йода.
Их парциальные давления:
![]() и
и ![]() .
.
По закону Дальтона: р=р1+р2.
Получим: ![]() , откуда
, откуда ![]() ; б=0,12.
; б=0,12.
Пример 7. Какое давление создают 2 г азота, занимающие объем V=820 см3 при температуре t=70 С?
Решение. Идеальные газы подчиняются уравнению состояния Менделеева-Клапейрона
![]()
,где p-давление газа, V - объем газа, Т - абсолютная температура газа, m - масса газа, М - масса одного киломоля газа, R - универсальная газовая постоянная, m/M– число киломолей газа.
Из уравнения имеем: ![]() =2⋅10-3⋅8,31⋅103⋅280/(28⋅820⋅10-6)=2,03⋅105 Па.
=2⋅10-3⋅8,31⋅103⋅280/(28⋅820⋅10-6)=2,03⋅105 Па.
Пример 8. Определить сколько киломолей и молекул водорода содержится в объеме 50 м3 под давлением p=767 мм рт. ст. при температуре t=180 С. Какова плотность и удельный объем газа?
Решение. На основании уравнения Менделеева-Клапейрона -
![]()
Устанавливаем число киломолей н, содержащихся в объеме V. Зная p - давление, V-объем, T - температуру газа, R - молярную газовую постоянную можно определить н:
н![]() кмоль
кмоль
Число молекул, содержащихся в данном объеме, находим, используя число Авогадро NA. Общее количество молекул, находящихся в массе m данного газа, может быть установлено, так как известно число киломолей н.
N=нNA
Подставляя в формулу число киломолей, устанавливаем число молекул, содержащихся в объеме:
N=2,11⋅6,02⋅1026=12,7⋅1026
Плотность газа определяем из уравнения Менделеева-Клапейрона:
![]() ;с=
;с=![]()
Подставляя числовые значения в единицах СИ в формулу, определим плотность газа
с=767⋅1,33⋅102⋅2/8,31⋅103⋅291=8,44⋅10-2 кг/м3
Удельный объем газа d определяем из уравнения Менделеева-Клапейрона:
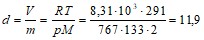 м3/кг
м3/кг
Пример 9. В баллоне объемом 10 л находится гелий под давлением p1=1 МПа и температуре T1=300 К. После того, как из баллона было взято m=10 г гелия, температура в баллоне понизилась до T2=290 К. Определить давление гелия, оставшегося в баллоне.
Решение. Для решения задачи воспользуемся уравнением Менделеева –Клапейрона, применив его к конечному состоянию газа:
![]() ,
,
Из уравнения выразим искомое давление р2:
![]()
Массу гелия m2 выразим через массу m1, соответствующую начальному состоянию, и массу m гелия, взятого из баллона:
m2=m1-m.
Массу гелия m1 найдем также из уравнения Менделеева-Клапейрона, применив его к начальному состоянию:
![]()
Подставляя массу m1, а затем полученное m2, найдем
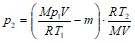
Или после преобразования и сокращения:
![]()
![]() Па
Па
Пример 10. В сосуде емкостью 8,3 л находится воздух при нормальном давлении и температуре T1=300 К. В сосуд вводят 3,6 г воды и закрывают крышкой. Определить давление в сосуде при T2=400 К, если вся вода при этой температуре превращается в пар?
Решение. Давление в сосуде складывается из давления воздуха, нагретого до температуры Т1, и давления водяных паров при той же температуре.
Из объединенного газового закона ![]()
По закону Дальтона для смеси газов р=р1+р2 найдем давление газа в сосуде:
![]()
Где р0=1,013⋅105 Па. Тогда
![]() Па
Па
Пример 11. В баллоне содержится кислород m1=80 г и аргон m2=320 г. Давление смеси р= 1МПа, температура Т=300 К. Принимая данные газы за идеальные, определить емкость V баллона.
Решение. По закону Дальтона давление смеси равно сумме парциальных давлений газов, входящих в состав смеси.
По уравнению Менделеева–Клапейрона парциальные давления кислорода р1 и аргона р2 выражаются формулами:
![]() и
и ![]() .
.
Следовательно, по закону Дальтона давление смеси газов:
p = р1+р2 или 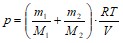 .
.
Откуда емкость баллона:
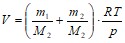
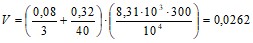 м3
м3
Пример 12. В сосуде объемом 2 м3 находится смесь m1=4 кг гелия и m2=2 кг водорода при температуре t=270 С. Определить давление и молярную массу смеси газов.
Решение. Воспользуемся уравнением Менделеева–Клапейрона, применив его к гелию и водороду:
![]() и
и ![]()

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |





