Для образцового средства измерений
![]() .
.
Для поверяемого средства измерений
![]()
Соотношение идеальных значений средних квадратических отклонений ![]() находят по заданному предельному значению для вероятности ошибки поверки
находят по заданному предельному значению для вероятности ошибки поверки ![]() . Для определения
. Для определения ![]() , кроме
, кроме ![]() , необходимо знать параметры распределений
, необходимо знать параметры распределений ![]() и
и ![]() . Ввиду того, что случайные погрешности имеют распределение, близкое к нормальному, среднее квадратическое отклонение, определенное по числу наблюдений, превосходящему 5, также распределено приблизительно нормально.
. Ввиду того, что случайные погрешности имеют распределение, близкое к нормальному, среднее квадратическое отклонение, определенное по числу наблюдений, превосходящему 5, также распределено приблизительно нормально.
Поэтому ![]() и
и ![]() можно оценить по графикам на чертеже приложения 1 при
можно оценить по графикам на чертеже приложения 1 при ![]() и выбранной вероятности
и выбранной вероятности ![]() .
.
Затем по таблицам приложения 4 при нормальном распределении средних квадратических отклонений случайных погрешностей образцового и поверяемого средств измерений и найденных ![]() находят
находят ![]() и по формуле (54) определяют
и по формуле (54) определяют ![]() .
.
1.7. Выбор предельного соотношения погрешностей при поверке средства измерений с корректировкой его показаний.
1. По разд. 3 вычислить ![]() ,
, ![]() ,
, 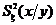 ,
, ![]() и
и ![]() . Выбрать коэффициенты доверительной вероятности
. Выбрать коэффициенты доверительной вероятности ![]() и
и ![]() .
.
2. Вычислить неполное соотношение погрешностей ![]() образцового и поверяемого средств измерений. При вычислении
образцового и поверяемого средств измерений. При вычислении ![]() учитывается только составляющие погрешности, изменяющиеся за время между двумя последовательными поверками
учитывается только составляющие погрешности, изменяющиеся за время между двумя последовательными поверками
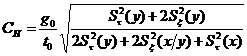 . (55)
. (55)
3. По ![]() ,
, ![]() ,
, ![]() и
и ![]() оценить вероятности
оценить вероятности ![]() и
и  , которые не должны превосходить заданных предельно допустимых значений
, которые не должны превосходить заданных предельно допустимых значений 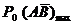 и
и  . Можно также сравнивать
. Можно также сравнивать ![]() с предельным значением
с предельным значением ![]() , установленным стандартами. В этом случае должно выполняться условие
, установленным стандартами. В этом случае должно выполняться условие ![]() .
.
Если эти условия выполнены, то соотношение ![]() , вычисленное по формуле (3), следует считать допустимым. Если условия не выполнены, то следует принять такие новые значения для
, вычисленное по формуле (3), следует считать допустимым. Если условия не выполнены, то следует принять такие новые значения для ![]() и
и ![]() при которых
при которых ![]() станет меньше
станет меньше ![]() или
или ![]() .
.
Затем снова вычислить реальное соотношение ![]() по формуле (3).
по формуле (3).
Пример: Выбор соотношений точностей при поверке средств измерений с корректировкой их показаний.
Пусть по источнику Г-излучения из 137Сs, являющемуся рабочим эталоном активности данного нуклида, поверяют аналогичный образцовый источник 1-го разряда. В результате сличения этих источников при каждой поверке определяют новое значение активности источника 1-го разряда. Найдем предел допускаемых соотношений доверительных погрешностей ![]() .
.
В результате теоретического и экспериментального исследования погрешностей установлено:
1. Случайный остаток систематической погрешности рабочего эталона характеризуется оценкой дисперсии ![]() .
.
2. Оценка дисперсии случайных погрешностей измерения активности нуклида рабочего эталона ![]() .
.
3. Оценка дисперсии случайных измерений активности нуклида в рабочем эталоне за межповерочный интервал, определяемая неточным знанием периода полураспада 137Сs, ![]() .
.
4. Оценка дисперсии, характеризующая неисключенные систематические погрешности метода поверки, определяемые неточностью знания отношения чувствительностей ионизационной камеры к Г-излучению 134Сs и 137Сs, ![]() .
.
11.5 Оценка дисперсии случайных погрешностей поверки.
![]()
11.6 Оценка дисперсии случайных измерений активности нуклида в поверяемом источнике во времени.
![]()
Исследования показали, что распределения погрешностей рабочего эталона и источников Г-излучения первого разряда близки к нормальному. Поэтому примем 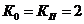 .
.
Выберем коэффициенты доверительной вероятности для эталона ![]() и поверяемого средства измерений
и поверяемого средства измерений 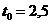 .
.
Вычислим неполное соотношение точностей ![]() по формуле (55)
по формуле (55)
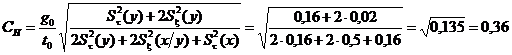
По табл. 13 для ![]() ;
; 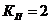 ;
; 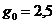 ,
, 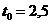 и
и 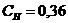 находим, интерполируя между
находим, интерполируя между ![]() и
и ![]() , вероятности событий при поверке
, вероятности событий при поверке ![]() ,
, ![]() ,
, ![]() .
.
Вычисляем 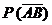
![]() .
.
Результаты расчета показывают, что вероятности ошибок поверки ![]() и
и ![]() достаточно малы, и поэтому соотношение
достаточно малы, и поэтому соотношение 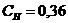 нас удовлетворяет.
нас удовлетворяет.
Определим реальное соотношение доверительных погрешностей эталонного и поверяемого по нему источников по формуле (3).
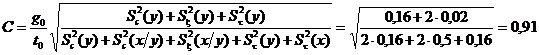
Таким образом, реальное соотношение доверительных погрешностей, равное 0,91, в данном случае допустимо.
12 Межповерочные (межкалибровочные) интервалы средств измерения (МПИ).
12.1. Основные положения и определения.
МПИ называется промежуток времени или наработка между двумя последовательными поверками СИ.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 |





