2.  Вычисляют оценку третьего центрального момента без далеко отстоящих наблюдений

. (41)

3.  Вычисляют оценку четвертого центрального момента и оценку асимметрии без далеко отстоящих наблюдений

, (42)

. (43)

Если , (44)

где 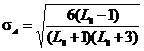, (45)

то распределение погрешностей по ансамблю с. и. можно считать симметричным, а в дальнейшем расчете принять .

4.  Вычисляют оценку эксцесса без далеко отстоящих наблюдений

. (46)

5.  В случае симметричного распределения погрешностей дальнейший расчет соотношения пределов допускаемых погрешностей проводят в следующем порядке.

Вычисляют по формуле (4) нормированное отклонение для проверяемых с. и.

Находят показатель формы распределения . Для этого следует воспользоваться чертежом приложения 2, где приведена зависимость коэффициента от эксцесса. – определяют по формуле (46). Далее расчет ведут, как указано в пп. 4.7.7 – 4.7.9.

6.  В тех случаях, когда условие симметричности (44) не выполняется, дальнейший расчет соотношения точностей проводят в следующем порядке.

Вычисляют оценки правостороннего и левостороннего первых моментов относительно моды

,

,

где – мода;

– наблюдения, находящиеся правее моды;

– наблюдения, находящиеся левее моды;

, – число наблюдений правее и левее моды, соответственно.

Если часть наблюдений попадает в интервал гистограммы, определяющий моду, то половину из них относят к правосторонним, половину к левосторонним моментам.

Вычисляют оценки правостороннего и левостороннего вторых моментов

,

.

Вычисляют оценки правостороннего и левостороннего четвертых моментов

,

. Где сумма?

Вычисляют оценки правостороннего и левостороннего эксцессов

,

.

По графику на чертеже приложения 2 находят соответствующие значения и .

Если заданные пределы допускаемой погрешности симметричны, то следует вычислить два значения нормированных отклонений

,

.

Если требуется назначить пределы допускаемых погрешностей при постоянном нормированном отклонении, которые могут быть и несимметричны, то следует задать вероятность (см. п. 4.4.2). Далее по чертежу приложения 1 следует выбрать из двух значений нормированных отклонений , соответствующего и , соответствующего – большее, т. е. .

Тогда

,

.

7.  Для определения характеристики распределения погрешностей образцового средства измерений следует использовать указания п. 4.4, если оценки проводятся теоретически, или п. 4.5, если оценку проводят по ансамблю средств измерений.

Вычислить по формуле (4) нормированное отклонение для образцовых средств измерений в данной поверяемой точке, если для них задан предел допускаемой погрешности.

Если предел допускаемой погрешности не задан, то следует оценить эксцесс (Э) теоретически по п. 3.9 или экспериментально по п. 4.6.4, затем, задавшись по чертежу приложения 1 найти , которые соответствуют на чертеже.

Соотношение нормируемых погрешностей образцового и поверяемого с. и. находим из формулы

.

8.  Оценка составляющих вероятности брака поверки. По табл. 1–5 приложения 4 при заданных значениях , и следует найти составляющие вероятности ошибок поверки и при равномерном распределении погрешностей образцового с. и.

По табл. 6–21 приложения 4, зная , , и , найти составляющие ошибок поверки и при нормальном распределении погрешностей образцовых с. и.

По табл. 21–35 при двойном – экспоненциальном распределении погрешностей образцовых с. и.

Вычислить значения вероятностей и при распределении погрешностей образцового с. и. с заданным

,

,

где

,

и – вероятности ошибок поверки при распределениях, между которыми проводится интерполяция.

9.  Значение вероятносте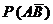й и сравнить с заданными пределами допускаемых вероятностей и . Если и , то выбранное соотношение следует считать удовлетворительным.

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49