11.4. Выбор максимально допустимого соотношения погрешностей поверяющего и поверяемого средств измерений.
Нормируемые характеристики.
Во всех случаях, когда установлены пределы допускаемых значений для характеристик точности средств измерений, выбор максимального соотношения нормируемых характеристик точности образцового и поверяемого средств измерений должен осуществляться на основе заданной вероятности ошибок поверки.
Нормируемыми характеристиками точности могут быть:
предел допускаемой систематической погрешности;
предел допускаемого среднего квадратического отклонения случайных погрешностей;
предел допускаемых случайных измерений показаний средств измерений за межповерочный интервал;
предел допускаемой общей погрешности.
Определение понятий.
1. События при поверке средств измерений (с. и.)
![]() – поступившее на поверку с. и. является фактически годным;
– поступившее на поверку с. и. является фактически годным;
![]() – поступившее на поверку с. и. фактически негодное;
– поступившее на поверку с. и. фактически негодное;
![]() – в результате поверки с. и. признано годным;
– в результате поверки с. и. признано годным;
![]() – в результате поверки с. и. признано негодным (забраковано).
– в результате поверки с. и. признано негодным (забраковано).
2. Вероятности событий, происходящих при поверке средств измерений:
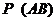 – фактически годное средство измерений будет правильно признано годным при поверке.
– фактически годное средство измерений будет правильно признано годным при поверке.
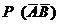 – фактически негодное средство измерений будет правильно забраковано при поверке.
– фактически негодное средство измерений будет правильно забраковано при поверке.
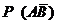 – фактически годное средство измерений будет забраковано при поверке.
– фактически годное средство измерений будет забраковано при поверке.
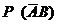 – средство измерений, погрешность которого превышает предельно допускаемое значение, будет признано годным при поверке.
– средство измерений, погрешность которого превышает предельно допускаемое значение, будет признано годным при поверке.
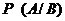 – средство измерений, признанное при поверке годным, действительно таковым является.
– средство измерений, признанное при поверке годным, действительно таковым является.
![]() . (32)
. (32)
Принципы определения соотношения нормируемых погрешностей образцового и поверяемого средств измерений.
В результате поверки с. и. признают годным или бракуют. Вследствие того, что образцовое с. и. и метод поверки обладают погрешностями, может оказаться, что решение, принятое в результате поверки, ошибочно. Правильные решения вместе с ошибочными составляют полную группу событий
![]() . (33)
. (33)
Вероятность правильных решений равна ![]() .
.
Вероятность ошибочных решений равна ![]() .
.
Вероятности возможных результатов поверки зависят от ![]() ,
, ![]() ,
, ![]() , показателей формы распределения погрешностей
, показателей формы распределения погрешностей ![]() для поверяющего и поверяемого средств измерений. Показатель
для поверяющего и поверяемого средств измерений. Показатель ![]() определяется эксцессом
определяется эксцессом ![]() .
.
При равномерном распределении погрешностей образцовых средств измерений (между установленными для них допусками) значения вероятностей ![]() и
и ![]() получаются большими, чем при других формах распределений погрешностей (для одних и тех же
получаются большими, чем при других формах распределений погрешностей (для одних и тех же ![]() ,
, ![]() ,
, ![]() ). С этой точки зрения это распределение будет наихудшим.
). С этой точки зрения это распределение будет наихудшим.
В приложении 4 приведены таблицы зависимостей ![]() ,
, ![]() ,
, ![]() и
и 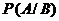 от
от ![]() ,
, ![]() ,
, ![]() и от показателя формы распределения
и от показателя формы распределения ![]() для поверяемых средств измерений при равномерном, нормальном и двойном – экспоненциальном распределениях погрешностей образцовых средств измерений. Для равномерного распределения
для поверяемых средств измерений при равномерном, нормальном и двойном – экспоненциальном распределениях погрешностей образцовых средств измерений. Для равномерного распределения ![]() для нормального распределения
для нормального распределения ![]() , для двойного экспоненциального
, для двойного экспоненциального ![]() . Используя указанные таблицы, можно при заданных
. Используя указанные таблицы, можно при заданных ![]() ,
, ![]() ,
, ![]() и вероятности
и вероятности ![]() или
или ![]() определить
определить ![]() и остальные вероятности, входящие в формулу (33). При
и остальные вероятности, входящие в формулу (33). При ![]() следует использовать только
следует использовать только ![]() . При С< 0,5 можно использовать
. При С< 0,5 можно использовать ![]() или
или ![]() .
.
Методика выбора соотношений пределов допускаемых погрешностей С можно подразделить на три вида: предварительную (теоретическую) оценку, ориентировочный расчет, уточненный расчет. Выбор той или иной методики производят в зависимости от объема предварительной информации.
Предварительная (теоретическая) оценка соотношения нормируемых погрешностей образцового и поверяемого средств измерений.
1. Предварительная (теоретическая) оценка значения С может быть сделана в процессе проектирования и при испытаниях одного-трех экземпляров средств измерений данного типа.
Теоретически оценить характеристики распределения погрешностей поверяемого средства измерений можно, воспользовавшись для этого указаниями п. 3.3.
2. Далее, задавшись вероятностью 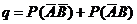 и используя вычисленное по формуле (31) значение
и используя вычисленное по формуле (31) значение ![]() , следует найти по графику на чертеже приложения 1 коэффициент доверительной вероятности (нормированное отклонение)
, следует найти по графику на чертеже приложения 1 коэффициент доверительной вероятности (нормированное отклонение) ![]() , а затем по формуле (4) вычислить теоретически обоснованный предел допускаемых погрешностей поверяемого средства измерений.
, а затем по формуле (4) вычислить теоретически обоснованный предел допускаемых погрешностей поверяемого средства измерений.
3. Затем следует оценить соотношение пределов допускаемых погрешностей. При этом для погрешностей образцового средства измерений используют гипотезу о равномерном распределении погрешностей. Если ![]() , то для распределения погрешностей по ансамблю поверяемых с. и. используют гипотезу о нормальном распределении (
, то для распределения погрешностей по ансамблю поверяемых с. и. используют гипотезу о нормальном распределении (![]() ). Если
). Если ![]() >2,5, то нужно использовать гипотезу о двойном экспоненциальном распределении (
>2,5, то нужно использовать гипотезу о двойном экспоненциальном распределении (![]() ).
).
Задают предельно допускаемое значение вероятности ![]() или
или ![]() . По таблицам приложения 4, используя известные значения
. По таблицам приложения 4, используя известные значения ![]() ,
, ![]() ,
, 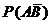 , находят С,
, находят С, ![]() ,
, ![]() , а если задано
, а если задано ![]() , то следует найти
, то следует найти ![]() ,
, ![]() .
.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 |





