Оценка дисперсии среднего арифметического случайных погрешностей равна
![]() .
.
3. По значению ![]() и заданной вероятности
и заданной вероятности ![]() (см. п. 4.4.2) при помощи номограммы на чертеже приложения 1 находят
(см. п. 4.4.2) при помощи номограммы на чертеже приложения 1 находят ![]() , а затем вычисляют по формуле предельную погрешность метода поверки
, а затем вычисляют по формуле предельную погрешность метода поверки ![]() .
.
Далее по графику на чертеже приложения 2 по значению ![]() находят показатель
находят показатель ![]() формы распределения погрешностей метода поверки.
формы распределения погрешностей метода поверки.
После этого следует воспользоваться положениями п. 4.5 для оценки характеристик распределения погрешностей поверяемых средств измерений и определения соотношения ![]() и вероятностей ошибок поверки.
и вероятностей ошибок поверки.
4. При ![]() следует определить предельную погрешность метода поверки.
следует определить предельную погрешность метода поверки.
Для этого вычисляют оценки дисперсии и эксцесса общей погрешности
![]() , (51)
, (51)
![]() , (52)
, (52)
![]() . (53)
. (53)
Таблица 3
Поверяемый миллиамперметр М-24 на 100 мА класса точности 1 | Образцовый амперметр М-104 (диапазон 0–150 мА) класса точности 0,2 | Вероятности составляющих ошибок поверки | ||||||||||
Поверяемая точка шкалы | Предел допускаемых абсолютных погрешностей, мА |
|
|
|
| Точка шкалы | Предел допускаемых абсолютных погрешностей, мА |
|
| Наименьшее |
|
|
20 40 60 80 100 | 1* | – 0,9 – 0,2 + 0,7 + 0,4 + 0,4 | 4,8 5,8 4,0 3,3 3,2 | 1,2 1,0 1,4 1,75 1,8 | 3,1 3,5 3,8 3,6 3,0 | 20 40 60 80 100 | 0,3 | 3 | 2 | 3,0 | 0,00161 0,00105 0,00016 0,00006 0,00085 | 0,00305 0,00195 0,00051 0,00029 0,00190 |
Сумма вероятностей ошибок поверки Среднее арифметическое вероятностей ошибок поверки | 0,00373 0,00075 | 0,00770 0,00154 |
В соответствии с п. 4.5.6:
суммарная вероятность: ![]() ;
;
суммарная вероятность: ![]() .
.
Таблица 4
Поверяемый миллиамперметр М-24 на 100 мА класса точности 1 | Образцовый амперметр М-104 (диапазон 0–150 мА) класса точности 0,2 | Вероятности составляющих ошибок поверки | |||||||||||
Поверяемая точка шкалы | Предел допускаемых абсолютных погрешностей, мА |
|
|
|
| Точка шкалы | Предел допускаемых абсолютных погрешностей, мА |
|
|
|
|
|
|
20 40 60 80 100 | 1 | – 0,9 – 0,2 + 0,7 + 0,4 + 0,4 | 4,8 5,8 4,0 3,3 3,2 | 1,2 1,0 1,4 1,75 1,8 | 3,1 3,5 3,8 3,8 3,0 | 20 40 60 80 100 | 0,3 | – 1,3 – 0,6 – 0,6 – 0,4 0 | 6,0 4,3 5,0 4,4 4,2 | 6,5 5,0 4,5 4,0 4,0 | 1,0 1,3 1,25 1,3 1,3 | 0,0018 0,0013 0,00016 0,00007 0,0011 | 0,0070 0,0046 0,0021 0,0016 0,0066 |
Сумма вероятностей ошибок поверки Среднее арифметическое вероятностей ошибок поверки | 0,00443 0,0009 | 0,0219 0,0044 |
В соответствии с п. 4.5.6 настоящей методики:
суммарная вероятность: ![]() ;
;
суммарная вероятность: ![]() .
.
Затем, задавшись ![]() и зная
и зная ![]() по номограмме на чертеже приложения 1 находят
по номограмме на чертеже приложения 1 находят ![]() и по формуле 4 вычисляют предельную погрешность поверки.
и по формуле 4 вычисляют предельную погрешность поверки.
Если ![]() задано, то отношение
задано, то отношение ![]() находят по формуле (3). Если
находят по формуле (3). Если ![]() не заданно, то отношение
не заданно, то отношение ![]() находят по заданным предельным значениям вероятностей
находят по заданным предельным значениям вероятностей 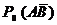 и
и 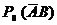 ,
, ![]() выбранному
выбранному ![]() и показателю формы распределения
и показателю формы распределения ![]() погрешностей поверяемого с. и., найденному из графика на чертеже приложения 2 по
погрешностей поверяемого с. и., найденному из графика на чертеже приложения 2 по ![]() . Для этого используют таблицы приложения 4.
. Для этого используют таблицы приложения 4.
1.6. Выбор соотношения нормируемых погрешностей образцового и поверяемого средств измерений с преобладающими случайными погрешностями.
1. Для средств измерений, у которых преобладают случайные погрешности, нормируют пределы допускаемых средних квадратических отклонений. Поэтому соотношение точностей ![]() равно отношению пределов допускаемых средних квадратических отклонений образцового и поверяемого средств измерений. Это соотношение является произведением двух величин
равно отношению пределов допускаемых средних квадратических отклонений образцового и поверяемого средств измерений. Это соотношение является произведением двух величин
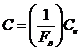 . (54)
. (54)
Первый член произведения ![]() характеризует рассеяние оценок дисперсий образцового и поверяемого средств измерений вследствие того, что эти оценки сделаны по ограниченному числу наблюдений
характеризует рассеяние оценок дисперсий образцового и поверяемого средств измерений вследствие того, что эти оценки сделаны по ограниченному числу наблюдений ![]() . При
. При 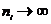
![]() . Значение
. Значение ![]() находят из таблицы распределения Фишера при заданной вероятности
находят из таблицы распределения Фишера при заданной вероятности ![]() , числах наблюдений
, числах наблюдений ![]() и
и ![]() и оценках дисперсий
и оценках дисперсий ![]() ,
, ![]() .
.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 |





