Если отношение С окажется большим 0,5, то, если было задано ![]() , следует снова задать предельно допускаемое значение, но только для
, следует снова задать предельно допускаемое значение, но только для ![]() . Далее по таблицам приложения 4, используя те же значения
. Далее по таблицам приложения 4, используя те же значения ![]() ,
, ![]() и заданное значение
и заданное значение ![]() , найти новые значения С,
, найти новые значения С, ![]() и
и ![]() . Эти значения следует считать окончательными.
. Эти значения следует считать окончательными.
4. После этого вычисляют наибольший предел допускаемых погрешностей для образцового средства измерений, которое можно применить для данного средства измерений. Его находят из равенства
![]() .
.
1.2. Ориентировочный расчет соотношения нормируемых погрешностей образцового и поверяемого средств измерений.
1. Ориентировочный расчет соотношения нормируемых погрешностей образцового и поверяемого с. и. проводят в тех случаях, когда имеется возможность собрать статический материал о распределении погрешностей по ансамблю, состоящему из 11–20 экземпляров поверяемых средств измерений. Такой объем статистических данных позволяет вычислить оценку дисперсии для погрешностей ансамбля и определить нормированное отклонение ![]() , которое затем используют при определении С и
, которое затем используют при определении С и ![]() . При этом распределение погрешностей образцовых средств полагают равномерным, а поверяемых (в зависимости от значения
. При этом распределение погрешностей образцовых средств полагают равномерным, а поверяемых (в зависимости от значения ![]() ) – нормальным или двойным экспоненциальным (см. п. 4.4.3). Расчет проводят в порядке, изложенном ниже.
) – нормальным или двойным экспоненциальным (см. п. 4.4.3). Расчет проводят в порядке, изложенном ниже.
2. Вычисляют оценку дисперсии погрешностей ансамбля поверяемых средств измерений. Для этого следует поверить 11–20 работоспособных экземпляров с. и. исследуемого типа по одному образцовому с. и. Если с. и. поверяют в нескольких точках шкалы, то они должны быть одинаковыми для всех экземпляров с. и. При поверке каждого с. и. и в каждой поверяемой точке следует произвести не менее четырех наблюдений.
3. Определяют, можно ли считать случайные погрешности существенными для с. и. данного типа. Для этого оценивают значимость дисперсии случайных погрешностей по сравнению с дисперсией систематических погрешностей по ансамблю, как описано в приложении 5.
4. Если для поверяемых с. и. задан предел допускаемой погрешности, то по формуле (4) следует вычислить нормированные отклонения ![]() в изучаемых точках их диапазона. Далее по графику на чертеже приложения 1, предполагая распределение погрешностей по ансамблю поверяемых с. и. при
в изучаемых точках их диапазона. Далее по графику на чертеже приложения 1, предполагая распределение погрешностей по ансамблю поверяемых с. и. при ![]() нормальным (
нормальным (![]() ), а при
), а при ![]() >2,5 двойным экспоненциальным (
>2,5 двойным экспоненциальным (![]() ), найти вероятность
), найти вероятность ![]() (см. пункт 4.4.2). Если предел допускаемой погрешности не задан, то, назначив
(см. пункт 4.4.2). Если предел допускаемой погрешности не задан, то, назначив ![]() , следует определить
, следует определить ![]() , а затем по формуле (4) вычислить предел допускаемой погрешности.
, а затем по формуле (4) вычислить предел допускаемой погрешности.
5. Оценивают требуемое отношение пределов допускаемых погрешностей образцового и поверяемого с. и. как указано в п. 4.4.3.
6. Для выбора отношения С нормируемых погрешностей образцового и поверяемого средства измерений при поверке в нескольких точках шкалы и при условии, что результаты поверок в каждой из точек взаимонезависимы, вычисляют среднее значение вероятности признания заведомо годного прибора годным.
![]() ,
,
где L – число поверяемых точек; 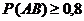 .
.
Затем по заданной вероятности ![]() находят среднюю вероятность ошибки 1-го рода
находят среднюю вероятность ошибки 1-го рода ![]()
![]() . (34)
. (34)
Далее, используя ![]() , по таблицам приложения 4 находят С.
, по таблицам приложения 4 находят С.
1.3. Уточненный расчет соотношения нормируемых погрешностей образцового и поверяемого по нему средств измерений.
1. Уточненный расчет соотношения нормируемых погрешностей образцового и поверяемого с. и. С проводят в тех случаях, когда возможно собрать данные о погрешностях приблизительно 100 экземпляров поверяемых средств измерений и оценить характеристики их распределения, а также экспериментально оценить форму распределения погрешностей образцового с. и. Имея эти данные, вычисляют ![]() ,
, ![]() ,
, ![]() и определяют
и определяют 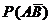 и
и 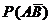 . Последние затем сравнивают с пределами допускаемых значений этих вероятностей
. Последние затем сравнивают с пределами допускаемых значений этих вероятностей 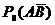 и
и 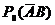 .
.
2. Все данные о погрешностях должны соответствовать одному и тому же номинальному значению физической величины. Если с. и. поверяется в нескольких точках шкалы, то эти точки должны быть одинаковыми для всех экземпляров с. и.
Могут быть использованы результаты измерений образцовым прибором при поверке ансамбля поверяемых мер или приборов или результаты измерения ансамблем поверяемых приборов величины, воспроизводимой образцовой мерой. Ансамбль, включающий около 100 однотипных с. и., будем называть большим ансамблем.
11–12 экземпляров с. и. (малый ансамбль) должны быть исследованы более тщательно. В каждой из поверяемых точек этих с. и. должно быть сделано по 11–20 наблюдений. Эти наблюдения следует проводить в несколько групп – по 4–5 наблюдений в группе.
3. Определение характеристик распределения систематических и случайных погрешностей.
Оценка средних арифметических:
а) по каждому с. и. в одной поверяемой точке шкалы
![]() , (35)
, (35)
б) по всему ансамблю с. и. в одной и той же поверяемой точке
![]() , (36)
, (36)
где ![]() ;
; ![]() – число средств измерений.
– число средств измерений.
Если для каждого из ![]() экземпляров с. и. проводится по одному наблюдению, то
экземпляров с. и. проводится по одному наблюдению, то
![]() .
.
Оценка дисперсии распределения случайных погрешностей для одной и той же поверяемой точки
![]() .
.
Оценка дисперсии распределения систематических погрешностей по ансамблю с. и.
![]() . (37)
. (37)
Если число наблюдений для всех с. и. равно друг другу, т. е. ![]() , то
, то
![]() . (38)
. (38)
4. Порядок дальнейшего расчета соотношения нормируемых погрешностей определяется соотношением систематической и случайной составляющих в погрешности с. и. рассматриваемого типа.
1.4. Определение соотношения нормируемых погрешностей поверяющего и поверяемого средств измерений при преобладании в погрешности средства измерений систематической составляющей.
1. Проверяют, имеются ли в распределении погрешностей по большому ансамблю отдельные далеко отстоящие погрешности. Если задано предельно допускаемое значение погрешности с. и. ![]() , то далеко отстоящей считается погрешность, удовлетворяющая неравенству
, то далеко отстоящей считается погрешность, удовлетворяющая неравенству
![]() . (39)
. (39)
Кроме того, на гистограмме распределения погрешностей по ансамблю с. и. между компактной частью и далеко стоящими наблюдениями будет область с нулевой частостью.
Если далеко отстоящие погрешности имеются, то следует заново вычислить оценку дисперсии (второго центрального момента) без этих погрешностей
![]() , (40)
, (40)
где ![]() – число погрешностей, оставшихся после исключения далеко отстоящих.
– число погрешностей, оставшихся после исключения далеко отстоящих.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 |





