где a - неизвестный параметр.
2. Для одномерного логнормального распределения:
где 
Максимально правдоподобная оценка среднего 
по Ачисону и Брауну:
и 
e=2,718…;
3. При наличии аномальных наблюдений принимают во внимание рекомендации Диксона и Масси по оцениванию среднего xДМ и стандартного отклонений SДМ по загрязненным выборкам. В качестве xДМ и SДМ в зависимости от степени загрязнения выборки используются обычное среднее арифметическое 
и медиана Me, обычное стандартное отклонение S и оценка по размаху:
и 
4. По бимодальной выборке наблюдений. Методом подтверждаем бимодальность распределения. Для каждой
локальной совокупности данных приемами 1 - 3 строим доверительные интервалы.
5. По устойчивым винзоризованным выборкам:
x1 ≤ x2 ≤ … ≤ xn.
Процедура g-винзоризации заключается в замене g первых членов на (g+1)-й член, а g последних членов - на (n-g)-й член:
Z1 = Z2 = … =Zg ≤ xg+2 ≤ … ≤ xn-g-1 ≤ xn-g =
= xn-g+1 = … =Zn-1=Zn;
и 
и 
h=n-2g,
где 
- квантиль распределения Стьюдента при h-1 степенях свободы;
6. Для выборочных данных с пропущенными наблюдениями. Для «восстановления» пропущенных наблюдений используют рекомендации А. Афифи и С. Эйзена, а затем строят доверительныеинтервалы, применяя приемы 1—5.
7. По угловым ориентированным наблюдениям:
- угловые замеры в градусах;
и 
при 
и 
где a0 неизвестный угловой параметр, градусы (например, азимут падения рудной зоны.
§ 2. Интервальные оценки сложных геологических переменных
1. Для прогнозных ресурсов изученного рудоносного поля. Расчеты минеральных ресурсов Q осуществляется по формуле:
где C - содержание полезного компонента, %; M - мощность рудной залежи; м; L - протяженность рудной залежи по простиранию, м; h - протяженность рудной залежи по вертикали, м; d - объемная масса руды, т/м3; KH - коэффициент надежности.
По трем переменным C, M и L в отдельности находят интервальные оценки (см. выше).
Сочетание вариантов:
приводит к n = 3x3x3 = 27 оценкам прогнозных ресурсов:
(при 
);
(при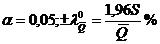 
);
2. Для прогнозных ресурсов новых рудоносных полей. Расчеты минеральных ресурсов QН, новых рудоносных полей осуществляются по формуле:
где SH и DH - соответственно площадь нового рудоносного поля и доля площади рудовмещающей толщи в ней; DP - доля рудной площади продуктивного горизонта от площади рудовмещающей толщи; pH - количество металла, приходящееся на единицу площади продуктивного горизонта (продуктивность) по имеющимся фактическим данным на новом рудоносном поле; kH - коэффициент надежности, устанавливаемый экспертным путем.
В формуле переменной является по крайней мере pH, т. е. определяется по исходным данным объема n ≥ 2 в новом рудоносном поле. Подставляя их в формулу, имеем 
локальных определений прогнозных ресурсов 
:
и
и 
3. Для прогнозных ресурсов по параметрам вторичных остаточных ореолов рассеяния элементов-индикаторов. Прогнозные ресурсы Q рассчитываются по формуле:
Q=kHq=kHp/40,
где k - коэффициент пропорциональности, устанавливаемый в каждом районе специальными опытно-методическими работами; H - целесообразная, по геологическим данным, глубина подсчета; q - продуктивность, выраженная в тоннах металла для слоя мощностью 1 м, q = 2,5р/100 = р/40; p - площадная продуктивность, 2,5 - усредненная объемная масса горных пород; 100 - коэффициент для перехода от весовых процентов к тоннам металла.
В формуле прогнозных ресурсов площадная продуктивность p выступает в качестве переменной, что обусловливает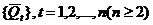 
определений прогнозных ресурсов:
и
и 
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
