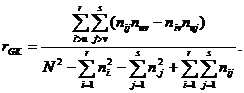
Коэффициент связи rGK, введенный Гудмэном и Красклом, изменяется в интервале от -1 до 1. Если X и Y связаны обратной зависимостью, то коэффициент отрицательный, в противном случае положителен. Чем слабее связь, тем ближе его величина к нулю.
Оценку значимости коэффициента связи rGK, т. е. проверку гипотезы H0: r = 0 выполняют путем сравнения его выборочного значения и стандартного отклонения. Для этого вычисляется верхняя граница дисперсии коэффициента rGK:
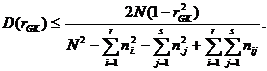
Гипотеза H0 отвергается при уровне значимости a, если r = 0 не принадлежит интервалу: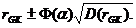 
Следует отметить, что, оперируя при проверке гипотезы верхней границей дисперсии, мы несколько расширяем область принятия нулевой гипотезы. Но это мера вынужденная, но необходимая, так как точное распределение используемых статистик связи неизвестно.
Если число градаций (классов) велико, то пользоваться таблицей сопряженности и соответствующими коэффициентами связи неудобно. В таких случаях оценивание тесноты и направления линейной связи выполняется с помощью так называемых ранговых коэффициентов.
Б). Ранжируемые данные. Процедура ранжирования - это расположение значений переменной в порядке возрастания и определение рангов каждого значения как его номер в этом упорядоченном ряду. При повторяющихся значениях для последних вычисляется усредненный ранг. Ранговую меру связи между X и Y (RX и RY - ранжированные переменные) можно определить так:
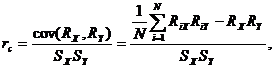
где RX, RY - средние арифметические рангов, а SX, SY - средние квадратические отклонения этих рангов. После преобразований получаем упрощенный вариант формулы:
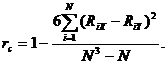
Показатель связи был введен Спирменом. Отсюда и его название - ранговый коэффициент корреляции Спирмена. Оценка существенности этого рангового коэффициента производится путем сравнения его выборочного значения с предельно допустимым значением ra, величина которого регулируется как числом наблюдений, так и уровнем значимости a. Имеются таблицы точного распределения коэффициента Спирмена, правда они не совсем удобны для пользования. Коэффициент корреляции Спирмена изменяется в интервале от -1 до 1, достигая крайних значений в случаях либо полной согласованности обоих рядов - RX и RY, либо их полной несогласованности.
3). Количественная геологическая информация.
Если измерения выполнены по пропорциональной шкале (шкале отношений), то полученные данные, в отличие от качественных и порядковых измерений, допускают использование при их обработке любых арифметических действий. Это обстоятельство позволяет опираться при вычислении выборочных коэффициентов связи не на частоты или ранги, а непосредственно на значения коррелируемых случайных величин. Тем самым обеспечивается полнота извлечения из результатов наблюдений необходимой, с точки зрения решаемой задачи, информации. Измеренные признаки можно рассматривать как непрерывные случайные величины.
Параметрический коэффициент парной корреляции - числовая характеристика силы линейной связи между случайными величинами. Коэффициент парной корреляции определяется как:
Свойства коэффициента корреляции:
1) -1£r(X, Y)£1, если коэффициент больше нуля, то X и Y - положительно коррелированные; если меньше нуля - отрицательно коррелированные;
2) r(X, Y)= r(Y, X);
3) X=a+bY Þ r(X, Y)=1, где a и b - константы;
4) X, Y - независимые случайные величины Þ r(X, Y)=0. Причем равенство r(X, Y)=0 является необходимым и достаточным условием независимости X и Y лишь в том случае, если двумерная случайная величина (X, Y) нормально распределена. Если вид распределения (X, Y) неизвестен, то при выполнении равенства r(X, Y)=0 говорят о некоррелированности X и Y.
Выборочный коэффициент корреляции r - оценка коэффициента корреляции по выборочным данным имеет вид:
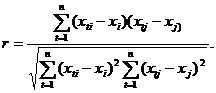
При малых объемах наблюдений r получается заниженным по сравнению с истинным значением коэффициента корреляции. Поэтому при n < 10 для r следует использовать оценку:
Проверка значимости r, т. е. проверка гипотезы о том, что в генеральной совокупности истинная корреляция двух случайных величин равна нулю [H0: r(X, Y)=0], осуществляется с помощью специальных таблиц процентных точек выборочного коэффициента корреляции ra, k (a - уровень значимости, k=n-2 - число степеней свободы), вычисленных при условии что X и Y распределены по двумерному нормальному закону.
Нулевая гипотеза H0: r(X, Y)=0 отклоняется, если r > ra, k (в противном случае принимается). Значимость выборочного коэффициента корреляции может быть оценена также с помощью таблиц квантилей распределения Стьюдента и F-распределения, а именно статистики 
в условиях нулевой гипотезы H0: r(X, Y)=0 распределена по закону Стьюдента с n-2 степенями свободы.
Аналогично, статистика F=r2(n-2)/(1-r2) или F'=(1+r)/(1-r) в условиях нулевой гипотезы H0: r(X, Y)=0 имеют F-распределения со степенями свободы: первая - 1 и (n-2), вторая соответственно (n-2) и (n-2).
4). Нелинейная корреляция.
В тех случаях, когда есть основания предполагать, что связь между исследуемыми переменными нелинейна, оценку тесноты связи следует выполнять с помощью корреляционного отношения или же коэффициента сопряженности. Оценка корреляционного отношения вычисляется следующим образом. Пусть исследуется зависимость Y от X. Разобьем множество наблюдаемых значений X на k классов (интервалов) и подсчитаем для каждого j-го класса среднее:
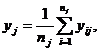
где nj - число точек, попавших в j-ый интервал,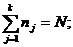 
yij - значение переменной Y, принадлежащие j-му интервалу группирования. Оценка корреляционного отношения rY|X находится по формуле:
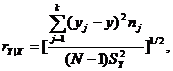
где y - оценка среднего; 
- оценка дисперсии переменной Y. Величина rY|X меняется в пределах от 0 до 1. Отметим, что в общем случае rY|X¹rY|X. Проверка гипотезы 
осуществляется на основе критерия:
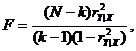
имеющего в условиях нулевой гипотезы F-распределение с (k-1) и (N-k) степенями свободы.
Если F > Fa, k-1,N-k, то нулевая гипотеза отвергается при уровне значимости a. Разность 
где r - коэффициент линейной корреляции, может служить мерой линейной связи. Чтобы сделать статистически обоснованный вывод о существенной нелинейности исследуемой зависимости, необходимо вычислить критерий:
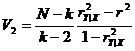
и сравнить V2 c Fa, k-2,N-k.
Если V2 < Fa, k-2,N-k, то нет никаких оснований отказаться от линейной модели.
Понятие корреляционного отношения может быть обобщено на многомерный случай. Если значения переменных Y и X сведены в таблицу сопряженности:
X\Y | B1 | … | Bs | S |
A1 | n11 | … | n1s | n1. |
… | … | … | ….. | …. |
Ar | nr1 | … | nrs | nr. |
S | n.1 | … | n. s | N |
то проверку гипотезы о независимости можно выполнить с помощью критерия:
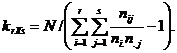
В условиях гипотезы о независимости величина krXs удовлетворительно аппроксимируется c2-распределением с (r-1)(s-1) степенями свободы. Если 
следует принятие гипотезы о зависимости переменных Y и X.
Оценка тесноты связи вычисляется по формуле:
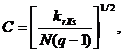
где C - коэффициент сопряженности (связанности); q=r, если r£s, и q=s, если r>s. Коэффициент C меняется в пределах от 0 до 1.
5). Частный коэффициент корреляции.
При исследовании взаимосвязи случайных величин xk и xl, входящих в систему {xj: j=1,…,m}, часто возникает подозрение, что величина парного коэффициента корреляции rkl определяется не столько степенью взаимозависимости величин xk и xl, сколько согласованным воздействием на них остальных образующих систему величин. Метод частной корреляции позволяет произвести "очистку" коэффициента корреляции rkl от влияния остальных величин, входящих в систему. Числовой характеристикой такой "очищенной" связи является частный коэффициент корреляции, измеряющий тесноту и направление связи между xk и xl при фиксированных значениях величин {xj: j=1,…,m; j¹k; j¹l}.
Если задана матрица парных коэффициентов корреляции:
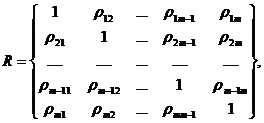
то частный коэффициент корреляции между случайными величинами xk и xl при фиксированных значениях всех остальных переменных определяется по формуле:
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
