Коэффициенты регрессии bj, выраженные в натуральном масштабе, можно представить в стандартизированной форме, что более удобно при их сравнении:

Здесь {Sxj, Sy - стандартные отклонения xi и y}. Величина и знак этих коэффициентов позволяют оценить интенсивность и направление влияния регрессоров на результирующую переменную. Абсолютная величина j-го коэффициента в стандартизированной форме показывает, на какую долю стандартного отклонения изменится среднее значение переменной Y при условии, что Xj возросло (уменьшилось) на величину Sxj, а остальные независимые переменные остались бы на прежнем уровне.

Если регрессоры можно отождествить с некоторыми природными факторами, то такого рода анализ регрессионной модели может оказаться эффективным средством решения генетических задач геологии. Но прежде чем приступить к содержательной интерпретации коэффициентов регрессии необходимо убедиться в статистической значимости последних.

Качество уравнения регрессии можно оценить следующим образом. Нулевая гипотеза:

H0: b1=…=bp=0

при альтернативе H1: b¹0 хотя бы для одного j£p. Для проверки используется критерий F:

где R вычисляется по формуле:

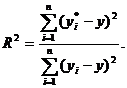
В условиях нулевой гипотезы критерий F имеет F-распределение со степенями свободы p и n-p-1. Если F>Fa, p,n-p-1, то нулевая гипотеза отвергается и принимается решение об удовлетворительном качестве соответствия регрессии эмпирическим данным.

Если уравнение регрессии служит для прогнозировании Y по {Xj}, то для повышении надежности рекомендуется добиться путем подбора соответствующего уравнения выполнение соотношения F>4Fa, p,n-p-1.

R2 можно трактовать как индикатор адекватности регрессионной модели. R2 оценивает ту долю изменчивости Y, которая "объясняется" регрессией. Для небольших n предлагается специальная коррекция R2, устраняющая его смещение. Нахождение исправленного значения выполняется следующим образом:

Отклонение нулевой гипотезы : H0: b1=…=bp=0 не означает, что среди набора регрессоров нет переменных, вклад которых в объяснение результирующей Y близок или равен нулю. Поэтому следующей задачей является проверка гипотез о равенстве нулю каждого из p коэффициентов регрессии: H0: bj=0 при альтернативе H0: bj¹0. Для проверки нулевой гипотезы используется критерий t=bj/Sbj, где

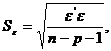
а (X'X)-1 - j-ый элемент диагонали матрицы (X'X)-1 (X - матрица эмпирических данных для независимых переменных). Если , где выбирается из таблиц распределения Стьюдента, то нулевая гипотеза отклоняется с уровнем значимости a, т. е. можно считать, что имеет место существенное уклонение от 0 коэффициента bj.

Выполнив такую проверку для всех коэффициентов bj, получаем возможность сосредоточить свое внимание на содержательном анализе тех из них, для которых нулевая гипотеза была отвергнута. Для оценки их точности полезно построить доверительные интервалы:

P{bj-ta, n-p-1Sbj£bj£ bj+ta, n-p-1Sbj}=1-a,

накрывающий с надежностью (1-a)*100% истинный коэффициент регрессии bj. Чем уже ширина такого интервала, тем "лучше" выборочная оценка bj, а значит и более надежна генетическая или иная интерпретация соответствующего регрессора.

При использовании уравнений регрессии в прогнозных целях полезно построить доверительные интервалы для предсказываемой переменной Y. Доверительный интервал для отдельного значения yi имеет границы:

где Sli - оценка стандартной ошибки прогноза в точке Xi:

где строка значений регрессоров в i-ой точке.

Если точность предсказания Y по набору регрессоров невелика, то обычно пытаются сменить вид функции (например, переходом от линейной к степенной), либо произвести ревизию регрессоров {Xj, j=0,1,…,k}. В последнем случае используют пошаговые процедуры, в основе которых лежат операции удаления или включения тех или иных регрессоров. Общее правило для включения или невключении переменной в множество регрессоров, сводится к выяснению вопроса, улучшается или нет предсказание по новому набору регрессоров {Xj, j=0,1,…,k, k+1}. Эта задача может быть сформулирована как проверка гипотезы

при альтернативе

где- частный коэффициент корреляции.

Проверку нулевой гипотезы проводят с помощью критерия:

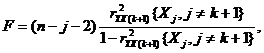
где - оценка частного коэффициента корреляции.

Если F>Fa,1,n-j-2, то принимается альтернатива

вклад переменной Xk+1 считается существенным и она присоединяется к набору регрессоров.

Процедура повторяется для всех переменных. В качестве наилучшего регрессора выбирается такой Xj, для которого,

т. е. является максимальным для всего набора регрессоров.

Далее последовательно рассматриваются все оставшиеся аргументы. Выбирается один из них, обладающий максимальным F. Он присоединяется к уже выбранным регрессорам. Процедура заканчивается, если значения F станут меньше критического.

Опираясь на этот критерий можно построить пошаговую процедуру, которую можно рассматривать как метод исключения. Сначала рассматривается максимально полный набор регрессоров, а затем производится их последовательное удаление (тех которые не способны предсказывать).

Регрессия наименьших абсолютных отклонений. При аппроксимации зависимой переменной y линейной комбинацией y*=a1x1+…apxp независимых переменных x1,…,xз с помощью уравнения регрессии параметры оцениваются из условия обращения в минимум средней суммы квадратов отклонений:

Но имеется ряд соображений в пользу другого критерия при построении регрессионной модели - критерия минимизации среднего абсолютного отклонения:

Эти соображения следующие:

1 - в ряде задач D является естественной мерой точности, не искажая величину отклонений, в то время как среднеквадратическое отклонение увеличивает роль больших отклонений и преуменьшает роль малых;

2 - регрессия по данному критерию более устойчива, чем по критерию минимума суммы квадратов отклонений, т. к. она менее сдвинута в сторону точек с большими отклонениями;

3 - метод нахождения y* прост и легко реализуем;

4 - метод наименьших квадратов естественен в случае нормального распределения.

Критерий наименьших абсолютных отклонений естественен в случае закона Лапласа (двустороннего экспоненциального) с плотностью 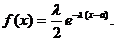Законы Гаусса и Лапласа близки, однако плотность закона Лапласа обладает большей островершинностью и весомостью хвостов.

Регрессия на ортогональных переменных.

Оценки, полученные на основе классической линейной модели, обладают тем недостатком, что с добавлением в модель новой независимой переменной все полученные ранее оценки необходимо пересчитывать. От такого недостатка свободна модель, в которой матрица X имеет ортогональные столбцы.

Если система векторов x,…,x линейно независима, то к ней можно применить процесс ортогонализации, в результате чего получим новую систему векторов:

……………………

В новых переменных общая регрессионная модель будет иметь вид:

В предположении нормального распределения ошибок строятся, как и в случае общей модели, соответствующие доверительные интервалы и доверительные области. Существенным достоинством перехода к ортогональным переменным является возможность провести регрессионный анализ в случае, когда столбцы матрицы X линейно зависимы. В этом случае матрица X'X вырождена и общая модель регрессии неприменима. В процессе ортогонализации векторов матрицы X с вырожденной матрицей X'X на некотором шаге j получим (zj, zj)=0. Это означает, что следующая система векторов (x1,…,xj-1,xj) линейно зависимая. Исключив вектор xj из рассмотрения, продолжаем ортогонализацию дальше. В результате ряд столбцов матрицы X будет исключен и останется матрица с линейно независимыми столбцами.

К недостаткам использования ортогональных переменных следует отнести необходимость пересчета всех коэффициентов при добавлении или исключении отдельных наблюдений.

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28