Часто задачи кластерного анализа подразделяют на два типа: 1- классификация сравнительно небольших по объему совокупностей многомерных наблюдений, когда их несколько десятков и 2 - классификация больших массивов многомерных наблюдений, когда их сотни и тысячи.
Задачи классификации делятся по типу априорной информации на три типа: 1 - число классов априорно задано, 2 - число классов неизвестно и его следует определить, а также 3 - число классов неизвестно, но его определение не входит в условие задачи.
Две последние ситуации приводят к построению иерархических деревьев – дендрограмм. Существует два типа иерархических деревьев – агломеративное и дивизимное. При этом выделяются три основные кластерные процедуры: 1 - иерархические агломеративные и дивизимные; 2 - параллельные, реализуемые с помощью итерационных алгоритмов; 3 - последовательные, реализуемые с помощью итерационных алгоритмов, причем на каждом шаге итерации привлекается небольшая часть наблюдений.
Кластерный анализ – совокупность методов классификации и разбивка объектов и многомерных наблюдений на однородные группы. Но трудно установить точные правила кластерного анализа, применяемые во всех ситуациях, и построить объективный критерий для сравнения кластеров, полученных с помощью различных процедур.
Кластер – скопление, пучок, группа элементов, характеризуемых каким-либо общим свойством. Методы их нахождения – это и есть собственно кластерный анализ.
Таксон – систематизированная группа любой категории. Методы их нахождения - численная таксономия.
Функция расстояния (метрика) – однозначная неотрицательная функция определенная для любых двух элементов, если соблюдаются следующие аксиомы:
1) d(x, y)³0 "x, y;
2) d(x, y)=0 тогда и только тогда, когда x=y (максимальная близость объекта с самим собой);
3) аксиома симметрии: d(x, y)=d(y, x);
4) аксиома треугольника: d(x, y)£d(x, z)+d(z, y).
Мера сходства (коэффициент сходства) – неотрицательная вещественная функция r(x, y), определенная для всех x и y, если соблюдаются следующие аксиомы:
1) 0£r(x, y)£1;
2) аксиома максимального сходства объекта с самим собой: r(x, x)=1;
3) аксиома симметрии: r(x, y)=r(y, x);
4) аксиома монотонности убывания коэффициентов сходства по функции расстояния: d(x, y)³d(x, y) Þ r(x, y)£r(x, y).
Дендограмма – одномерный граф, напоминающий дерево, который используется для изображения взаимных связей между объектами заданного множества. Объекты располагаются по иерархическим уровням так, чтобы подчеркнуть их взаимное сходство на основе измеряемых свойств. Объекты располагаются на равном расстоянии друг от друга, выбранном произвольно. Ветви дерева характеризуют иерархический порядок объектов.
Дендограф – двумерная дендрограмма. Дендрограф описывает зависимости как внутри групп объектов, так и между группами. В результате имеем более наглядное графическое изображение связей между объектами.
Агломеративная кластерная процедура – связана с вычислениями функций расстояний и мер сходства между всеми парами объектов и объединением на каждом шагу той пары, для которой достигается минимум (максимум) функций расстояний и мер сходства. Кластеризация осуществляется путем объединения первоначально разобщенных объектов.
Дивизимная кластерная процедура – связана с вычислениями функций расстояний и мер сходства между всеми парами объектов и объединением на каждом шагу той пары (группы) объектов, для которой достигается их максимум (минимум). Кластеризация осуществляется путем разграничения первоначально единой группы объектов.
Типы расстояний и меры сходства. Коэффициенты сходства или различий между многомерными наблюдениями подразделяются на три типа.
Первый тип – коэффициенты расстояния. Их общий вид:
![]() ,
,
где m – число компонент векторов x и y.
Второй тип – коэффициенты ассоциативности. Они предназначены для оценивания сходства между парами многомерных наблюдений, описываемых значениями признаков в виде двоичного кода (бинарными признаками). Общий вид коэффициентов ассоциативности (коэффициент общего сходства Гауэра):
![]() ,
,
где 0£Si£1 – сходство между состояниями признака i для многомерных наблюдений x и y; Wi – вес, приписываемый этому признаку.
Третий тип – коэффициенты корреляции (отношение ковариации двух переменных к произведению их стандартных отклонений):
![]() ).
).
Расстояния и меры сходства между многомерными геологическими наблюдениями:
1. Обычное евклидово расстояние:
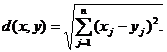
2. Обычное расстояние Махаланобиса:
![]()
где S – ковариационная матрица генеральной совокупности, из которой извлекаются многомерные наблюдения.
3. Хеммингово расстояние как мера наблюдений, задаваемых дихотомическими (0 и 1) признаками:
![]() .
.
Расстояния и меры сходства между геологическими объектами:
1. Минимальное локальное расстояние, измеряемое по принципу «ближайшего соседа»:
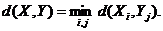
2. Максимальное локальное расстояние, измеряемое по принципу «дальнего соседа»:
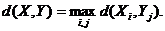
3. Расстояние центроидное:
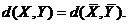
4. Среднее расстояние (средняя связь):
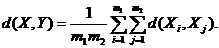
5. Хаусдорфово расстояние:
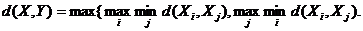
6. Расстояние Махаланобиса:
![]()
где S – оценка обобщенной ковариационной матрицы.
Расстояния и меры сходства можно ввести также для групп геологических объектов.
Глава IV. Интервальные оценки геологических переменных
Интервальные оценки геологических переменных характеризуют их точность при заданной надежности. Понятие «доверительный интервал» введено Дж. Нейманом и Е. Пирсоном. Так называют вычисленный по выборочным значениям интервал, который с заданной вероятностью (надежностью) Р = 1-α накрывает истинное, неизвестное исследователю значение параметра. В отличие от точечных оценок в виде одного числа интервальные оценки характеризуют нижнюю и верхнюю доверительные границы при заранее заданной надежности 1-α (α - риск, вероятность того, что истинное значение параметра не накрывает данный интервал).
Известны три основных типа интервального оценивания: доверительные интервалы по Нейману, основанные на частотной теории вероятностей; фидуциальные интервалы по Фишеру, использующие идеи, не охватываемые частотной теорией; доверительные интервалы по Байесу, основанные на теореме Байеса и на одной из форм постулата Байеса. Для применения последних интервальных процедур нужна априорная информация, чаще всего отсутствующая для реальных геологических ситуаций. Наиболее важные для геологических исследований неймановские доверительные интервалы можно разделить на интервалы для единственной геологической переменной и для набора переменных. Первые включают: точное оценивание параметров на основе достаточной статистики и стьюдентизации; асимптотическое оценивание параметров на основе первой производной или на основе второй и более высоких производных; оценивание параметров по расслоенным выборкам (методом повторных оценок) для нормально, логнормально и полимодально распределенных совокупностей данных.
Доверительные интервалы для набора геологических переменных включают: точное и асимптотическое оценивание параметров на основе стьюдентизации, оптимизационной основе, а также оценивание параметров по расслоенным выборкам для функций в виде произведений, отношений и сложных отношений геологических переменных. В качестве геологических переменных можно рассматривать: содержания основных и попутных компонент в руде, элементов-индикаторов в геохимических аномалиях, элементов-примесей в минералах; индикаторные отношения элементов, продуктивностей, прогнозных ресурсов по категориям Р3, Р2 и P1 запасов полезных ископаемых по категориям С2, С1, В и А; разнообразные кондиционные показатели разведки и освоения месторождений, показатели в поисковой и технологической минералогии, показатели осевой, продольной и поперечной зональности первичных и вторичных геохимических ореолов и потоков рассеяния, показатели мультипликативных и аддитивных геохимических суммарных ореолов и т. п.
Ниже приведены перспективные неймановские процедуры интервального оценивания по расслоенным выборкам.
§ 1. Интервальные оценки простых геологических переменных
Для получения интервальных оценок необходимо найти ряд характеристик выборочных распределений, а именно: среднее, стандартное отклонение, границы доверительного интервала Ниже эти характеристики приведены для различных распределений:
1. Для одномерного нормального распределения. Геологическая переменная - содержание компонента, мощность рудного тела и т. п. - замерена (опробована) в n точках:
![]()
![]()
![]() где
где 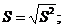
![]() и
и ![]()

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |




