Математические методы моделирования параметров геологических процессов и явлений (стр. 23 )

B=LT,

где Т - ортогональная матрица.

Этим свойством матрицы отображения можно воспользоваться, если заранее известны свойства факторов, которые желательно получить в конечном итоге.

Вращение в пространстве факторов позволяет зачастую уменьшить число тех факторов, от которых зависят исследуемые переменные. Существуют различные методы реализации вращения факторов: графические и аналитические. В основе их лежит наглядная интерпретация факторов и факторных нагрузок. Если представить себе факторные нагрузки как координаты точки в k-мерном пространстве факторов, а сами факторы считать ортогональными осями в этом пространстве, то преобразование факторного решения есть по существу вращение этих осей вокруг начала координат. Ясно, что это вращение можно выбрать бесконечным числом способов.

В основе графического метода вращения факторов лежит следующий принцип, который мы охарактеризуем на примере, когда исходное факторное отображение содержит только два фактора f1 и f2 Тогда переменные z1, ..., zn можно представить себе точками на плоскости, координаты которых равны факторным нагрузкам. Новые оси выбираются так, чтобы вблизи осей (факторов) лежало по возможности больше точек. Ясно, что угол поворота осей координат на плоскости этими условиями определяется приблизительно, так что графический метод вращения факторных осей является в сущности эвристическим.

При большем числе факторов рассматриваются всевозможные двумерные проекции многомерной картины, и произведение вращений в каждой плоскости, определяемой парой факторов, дает матрицу вращений факторов в многомерном пространстве.

Современные аналитические методы вращения факторов основаны на следующей идее. Применение ортогонального преобразования в пространстве факторов ведет к ортогональному преобра­зованию матрицы факторных нагрузок: матрица L преобразуется в матрицу М так, что выполнены условия:

где i=1, 2, …, n.

Возведя это равенство в квадрат и просуммировав по всем переменным, получим условие:

В качестве критерия наилучшего преобразования (1974 г.) предложил максимизировать величину:

Это объясняется тем, что теоретический верхний предел этой функции достигается в том идеальном случае, когда каждая переменная зависит лишь от одного фактора. Идея в настоящее время реализуется одним из двух методов «квартимакс» и «варимакс». Эти методы отличаются лишь способом выбора угла поворота, определяемого по некоторым формулам, исходя из коэффициентов матрицы факторных нагрузок.

§ 3. Методы Q-модификации факторного анализа

Q-модификация вскрывает взаимосвязи между объектами, а R-модификация анализирует взаимосвязи между переменными. Значения факторов, получаемые в R-модификации, в некоторой степени обеспечивают способы описания взаимосвязей между объектами; однако обычно эти связи основаны на неудовлетворительной мере сходства между объектами. Коэффициент ковариации или корреляции может оказаться не лучшей мерой сходства между 2-я объектами.

Основой Q-модификации факторного анализа является понятие сходства между объектами. Если найдено подходящее математическое определение коэффициента сходства, можно сконструировать матрицу сходства порядка N´N, отражающую степень сходства всех возможных пар из N объектов. Обычно N велико. Определение ранга этой матрицы путем разложения на собственные числа и собственные векторы может обеспечить адекватное описание объектов в терминах базисных векторов, число которых обычно значительно меньше, чем исходных переменных.

Основные методы Q-модификации:

1.  Q-метод Имбри (определяет сходство между объектами по близости относительных содержаний составных частей);

2.  метод главных координат Гувера (использует в качестве показателя сходства евклидово расстояние между объектами);

3.  комбинированный метод Бенери (сходство устанавливается на основе вероятностной таблицы).

После того как матрица сходства или связей получена, дальнейшие процедуры производятся аналогично с методом главных компонент с использованием вращения (варимакс и др.) или без него. Но интерпретация итоговых матриц принципиально отличается от таковой в R-модификации.

1. Q-метод Имбри.

Геологическая интерпретация. Исходные данные - матрица порядка N´p. Ее строки - геологические объекты, а столбцы - свойства объектов. Переменные рассматриваются в качестве неких составных частей объектов (окислы, минералы и т. п.). Часто сумма количеств этих составных частей равна постоянному значению во всех строках, т. к. обычно эти количества выражаются в долях. Одним из способов (но ни в коем случае не единственным) исследования объектов матрицы данных является рассмотрение их в качестве комбинаций составов некоторого числа крайних членов. Иначе говоря, можно представить себе ситуацию, когда составы объектов матрицы данных получают путем смешивания в разных пропорциях некоторых гипотетических или реальных объектов заданного состава. В этом случае можно описать каждый объект в терминах пропорций крайних членов, а не количеств составных частей.

Рассмотрим простой геологический пример. А именно, предположим, что в бассейн седиментации выносились осадки из 3-х рек. Допустим, что каждая река вносит разные ассоциации минералов. Поступая в бассейн, эти ассоциации под действием физико-седиментологических факторов смешиваются в разных пропорциях. Тогда любой образец осадка представляет собой смесь 3-х объектов - крайних членов. Предположим, что бассейн подвергся погружению и уплотнению, а образовавшаяся в результате осадочная порода доступна опробованию. Целью исследования является определение областей сноса материала и факторов, обусловивших накопление осадков.

За исключением редкого случая хорошей обнаженности, обычно бывает трудно определить области сноса непосредственно путем картирования. Но, используя концепцию крайних членов, это можно сделать с помощью анализа состава пород. Можно попытаться выразить каждый образец пород в виде долей составляющих его минеральных ассоциаций. Трудность состоит в том, что в большинстве случаев не известны ни число различных минеральных ассоциаций - крайних членов, ни их составы. Поэтому сформулируем цели Q-анализа следующим образом:

1.  Найти минимальное число k ассоциаций - крайних членов, в качестве комбинаций которых можно рассматривать наблюдаемые объекты.

2.  Определить составы крайних членов через содержания p составных частей.

3.  Описать каждый объект в терминах крайних членов, т. е. разделить объект на составляющие его компоненты - крайние члены.

Первая задача - нахождение минимального числа крайних членов - решается аппроксимацией матрицы данных матрицей меньшего ранга. Таким способом выявляется число линейно независимых строк и размерность системы.

Для решения второй задачи - определения составов крайних членов - необходимы дополнительные ограничения, т. к. существует бесконечно много наборов из k составов, одинаково пригодных для этой цели. Q-метод Имбри предназначен для нахождения таких крайних членов, которые характеризуются максимальной контрастностью составов, относительно наблюдаемых объектов. Эти крайние члены могут быть теоретическими, или их роль могут играть наиболее контрастные по составу объекты матрицы данных.

Третья задача - определение вклада каждого крайнего члена в каждый объект - решается путем нахождения и анализа матрицы факторных нагрузок.

Как упоминалось, основой Q-модификации факторного анализа является понятие сходства между объектами. Имбри и Парди предложили оценивать степень сходства двух объектов (xn и xm) через косинус угла между соответствующими вектор-строками матрицы данных:

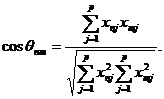
Абсолютное сходство будет для коллинеарных векторов (cosq=1). Причем абсолютные значения составных частей не учитываются при определении сходства: "большой" и "маленький" объекты считаются идентичными в случае пропорциональности их составных частей. Если в R-модификации факторного анализа исследуется ковариационная или корреляционная матрица, то в Q-методе Имбри - матрица {cosqij}.

Процедуры вычисления матриц факторных нагрузок и факторных значений могут производиться аналогично с методом главных компонент. Но следует обратить внимание, что в данном случае размерность матрицы сходства объектов может быть очень велика. Высокая размерность матрицы может приводить к значительным трудностям при вычислении собственных значений и векторов. Поэтому на практике используется более эффективная в вычислительном отношении процедура.

Число крайних членов. Эта задача эквивалентна установлению ранга матрицы сходства. Ранг k (число ненулевых собственных чисел) не может быть больше, чем p. Для реальных данных обычно k=p. Но достаточно часто можно удовлетворительно аппроксимировать матрицу значительно меньшим числом факторов. Поэтому для определения числа крайних членов используется "примерный" ранг матрицы. Для этого используется отношение собственного числа к следу матрицы, который равен N. Если это отношение показывает, что фактор вкладывает в решение ничтожную информацию, то этот фактор можно считать незначимым.

Геометрическое представление. Рассмотрим гипотетический пример, где исходные данные представлены в виде следующей матрицы, в которой сумма элементов строк равны 100.

Матрица исходных данных:

Собственные числа матрицы сходства:

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28