Таким образом, получается, что выбор уровня значимости и принятие решения после проверки гипотезы определяются рядом причин: характером альтернативы, сравнительной ценностью потерь от совершения ошибок первого и второго рода, выполнением условий, накладываемых на критерий, и т. п. Все это следует учитывать в процессе применения статистических методов в геологии и при интерпретации полученных результатов.

§ 2. Проверка гипотез о нормальном распределении

Большинство статистических критериев проверки гипотез применимо в предположении, что выборочные данные извлечены из нормально распределенной совокупности. Несмотря на то, что эти критерии широко используются в геологических исследованиях, нормальность распределений обычно не проверяется. Естественно, при таком применении статистических критериев полученные результаты далеко не всегда надежны.

Критерий проверки соответствия одномерного выборочного распределения заданному позволяет установить степень соответствия выборочных данных, состоящих из n значений случайной величины, заданной функции распределения F(x). Предполагается, что функция F(x) или не содержит никаких неизвестных параметров, или же они оцениваются по выборке, и вероятность события ξ<a может быть вычислена для любых вещественных значений a.

Критерий Пирсона c2. Критерий предназначен для проверки соответствия одномерного выборочного распределения заданному распределению F(x). Критерий Пирсона состоит в следующем. Предположим, что множество значений изучаемой случайной величины разбито на r непересекающихся частей S1,...Sr. Обозначим через pi вероятностную меру множества Si, вычисленную с помощью функции распределения F(x): pi=P(Si)=PF(xÎSi). По n выборочным данным можно определить частоты 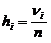попадания выборочных значений в соответствующие множества Si (ni - число попаданий выборочных значений в Si). Оказывается, что статистика

при n®¥ имеет асимптотическое распределение c2 с (r-1) степенями свободы. Таким образом, если при большом n статистика M превышает, при заданном уровне значимости a, критическое значение распределения c2 с (r-1) степенями свободы, то нет оснований считать, что исследуемая выборка извлечена из распределения с функцией распределения F(x). В противном случае можно считать, что выборочные данные находятся в соответствии с распределением, задаваемым функцией F(x).

Критерий Уэгла. Критерий предназначен для проверки соответствия эмпирического распределения многомерному нормальному. Этот критерий достаточно прост и соответствует интуитивному желанию исследователя ограничиться после некоторых преобразований проверкой нормальности распределений соответствующих одномерных характеристик. Имеется выборка X из N наблюдений над p-мерным вектором x=(x1,...xp). Вычисляется вектор средних значений и ковариационная матрица. Затем производятся некоторые преобразования значений X. Сущность критерия заключается в проверки нормальности распределений полученных в ходе преобразований одномерных характеристик. В случае принятия гипотез о нормальном распределении последних делается вывод о том, что выборка X извлечена из совокупности с многомерным нормальным распределением. В противном случае, нет оснований считать, что выборочные данные извлечены из совокупности с многомерным нормальным распределением.

Критерий Мардиа. Критерий предназначен для проверки соответствия эмпирического распределения многомерному нормальному. Этот критерий более сложен, но и более чувствителен, чем критерий Уэгла, к отклонению выборочного распределения от многомерного нормального. Используемые в нем статистики удобны при изучении влияния нарушения нормальности распределения на устойчивость известных критериев. Он сводится к вычислению двух статистик - одна из которых, имеет распределение c2, другая распределена по нормальному закону. Задаваясь одним и тем же уровнем значимости, сравниваем значения этих статистик с соответствующими критическими значениями. Если для обеих статистик вычисленные значения не превосходят соответствующее критическое значение, то гипотеза о том, что исследуемая выборка извлечена из совокупности с многомерным нормальным распределением принимается. В противном случае, нет оснований считать, что выборочные данные извлечены из совокупности с многомерным нормальным распределением.

В дальнейшем при проверки гипотез о параметрах распределения следует руководствоваться следующим правилом: в случае принятия гипотезы о соответствии эмпирического распределения нормальному можно использовать параметрические критерии, в противном случае, их использование неправомерно и следует обратиться к непараметрическим критериям. Наиболее надежный результат получается в случае, если несколько критериев (параметрических и/или непараметрических) критериев дают одинаковые результаты.

§ 3. Проверка гипотез о параметрах распределения

Критерий Вэлча (параметрический) предназначен для проверки гипотез о равенстве средних H0: a1=a2 при наборе альтернатив H1: a1¹a2. Здесь a1 и a2 - истинные средние для первого и второго объектов. Критерий использует предположение о нормальности распределений случайных величин (моделей изучаемых геологических признаков в сравниваемых объектах), об отсутствии аномальных наблюдений и некоторые другие. Для целей проверки гипотезы о равенстве средних при не очень малых объемах наблюдений n1 и n2 в выборках следует воспользоваться статистикой Вэлча:

t=,

где и - выборочные средние, а и - выборочные дисперсии. В условиях нулевой гипотезы H0: a1=a2 величина t распределена асимптотически по закону Стьюдента с m степенями свободы:

m=,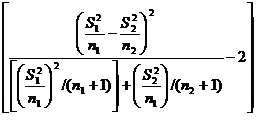

где символ [.] - взятие целой части от числа.

Нулевая гипотеза H0: a1=a2 принимается как подтвердившаяся, если вычисленная t-статистика Вэлча не превысит допустимый квантиль ta,m распределения Стьюдента при заданном уровне значимости a и m степенях свободы, т. е. если t £ ta,m. Проверяемая гипотеза отклоняется и принимаются альтернативы о существенности различий в средних:

H1: a1¹a2, если t > ta, m.

Критерий Вилкоксона (непараметрический) предназначен для проверки гипотез о равенстве средних H0: a1=a2 при наборе альтернатив H1: a1¹a2. Критерий Вилкоксона нечувствителен к нарушению условий нормальности распределения исходных геологических данных, к наличию аномальных значений и т. п. Предполагается, что элементы выборок взаимно независимы и подчиняются непрерывным распределениям. Процедура использования критерия Вилкоксона следующая. Из двух выборок исходных данных {xi}и {yi} составляется общий вариационный ряд объемом N=n1+n2 в порядке возрастания всех выборочных значений x и y. Далее нумеруются все члены этого ряда: 1,2,...,N (присваиваются ранги). Равным значениям (совпадающим членам) присваивают скорректированный средний ранг, представляющий собой среднее арифметическое рангов совпадающих (связанных) членов вариационного ряда. Статистика W критерия Вилкоксона представляет собой сумму рангов r, относящихся к членам меньшей по объему выборки (сумму ранговых чисел):

W=, при n1£n2.

Критические значения W1 и W2 определяются в зависимости от объемов наблюдений n1 и n2 в выборках.

Ситуация 1. Объемы выборки не превышают 25. По таблице для выбранного уровня значимости определяется нижнее критическое значение W1 и вычисляется верхнее критическое значение W2=2*MW-W1.

Ситуация 2. Объемы наблюдений в выборках превышают 25. Тогда критические значения W1 и W2 определяются по следующим приближенным формулам:

W1={} и

W2= n1(n1+n2+1)-W1,

где n1£n2, tµ/2 - квантиль гауссовского (нормального) распределения.

Для обеих ситуаций проверяемая гипотеза H0: a1=a2 принимается как не противоречащая исходным данным, если W1£W£W2, и отклоняется как не подтвердившаяся и, тем самым, принимаются альтернативы H1: a1¹a2, в противном случае.

F-критерий Фишера (параметрический) для проверки гипотез о равенстве дисперсий H0:= против набора альтернатив H1:¹, где и - истинные дисперсии для первого и второго объектов. Применение F-критерия Фишера базируется на предположении о нормальности распределения случайных величин c и h - моделей геологических признаков. Вычисляется F-статистика, представляющая собой отношение большей выборочной дисперсии к меньшей:

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28