Математические методы моделирования параметров геологических процессов и явлений (стр. 15 )

Если то дальнейшие вычисления прекращаются и все выделенные группы наблюдений рассматриваются как существенно отличающиеся одна от другой.

Если же 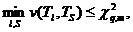то та пара групп Тl, Ts, на которой достигнуто это минимальное значение, объединяется в одну группу .

13. В результате число групп будет h-1, и процедура проверки продолжается для данного уменьшенного набора групп. Для этого достаточно вычислить значения критерия для всех возможных пар, которые образует с остальными h-2 группами. Значения критерия для тех пар, в которые не входит , можно взять из матрицы, определенной в пункте 11. Из всех этих значений критерия опять выбирается минимальное, которое сравнивается с критическим

14. Такая последовательная процедура проверки, использующая парные объединения, продолжается до тех пор, пока минимальное значение не превысит допустимое Необходимо отметить, что на практике бывает удобно в качестве критерия использовать отношение:

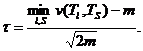
Процедура объединения прекращается как только будет достигнуто неравенство τ>3.

15. Полученные в результате группы наблюдений следует рассматривать как статистически однородные, отличающиеся одна от другой совокупности.

Глава VI. Методы восстановления зависимостей

§ 1. Дисперсионный анализ

Дисперсионный анализ - статистический метод исследования выборочных данных, проводимого с целью выявления и оценки степени влияния на изучаемую случайную величину различных одновременно действующих факторов.

В основе дисперсионного анализа лежит такое разложение общей изменчивости выборочных данных, при котором удается отделить изменчивость, связанную с некоторыми фиксируемыми исследователем факторами, от изменчивости, обусловленной, факторами, неконтролируемыми в данном эксперименте. Надежная статистическая оценка вклада контролируемых факторов возможна лишь при условии, что эксперимент (наблюдение) некоторым образом организован. Это определяет тесную связь дисперсионного анализа с планированием эксперимента. Если изменение хотя бы части контролируемых факторов может быть измерено количественно, пользуются комбинацией дисперсионного и регрессионного анализа.

При использовании дисперсионного анализа выборочные значения исследуемой случайной величины рассматривают как линейную комбинацию:

yi=x1ib1+…+xpibp+ ei,

где yi - результат наблюдения с номером i, {bj} - фиксированные в данном эксперименте факторы, {xji} - некоторые постоянные коэффициенты, ei - случайная нормально распределенная величина с нулевым математическим ожиданием и дисперсией s2.

Общим условием применения дисперсионного анализа является выполнение:

M(e)=0, M(ee*)=s2I,

где M(.) - математическое ожидание, I - единичная матрица. Т. е. величины {ei } - независимы и одинаково распределены.

А). Однофакторный дисперсионный анализ. Результаты измерений некоторого геологического признака на p объектах запишем в виде матрицы Y:

.

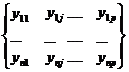На каждом объекте, соответствующем j-ой градации проверяемого фактора, произведено одинаковое число наблюдений, равное n. Значение исследуемого фактора - неизвестное постоянное. Предполагается, что наблюдения являются выборочными значениями случайных нормально распределенных величин x1,…,xj,…,xp с параметрами:

M(xj)=mj, D(xj)=s2 (равенство дисперсий).

В этом случае основное уравнение однофакторного дисперсионного анализа имеет вид:

yij=m+aj+eij,

где - m генеральное среднее, определяемое формулой aj - эффект j-ой градации исследуемого фактора, определяемый формулой aj=mj-m; eij - случайная независимая величина ("ошибка" наблюдения для i-го измерения величины xj), отражающая влияние на результаты эксперимента неконтролируемых в данном наблюдении факторов. Проверяемая статистическая гипотеза может быть сформулирована следующим образом: H0: a1=…=aj=…=ap. Т. е. влияние исследуемого фактора на всех объектах одинаково. Другими словами, в условиях H0 справедливо равенство: m1=…=mj=…=mp=m.

Проверка нулевой гипотезы осуществляется по следующей схеме.

1. Вычисляют выборочные средние:

и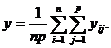

2. Находят суммы квадратов отклонений выборочных значений от соответствующих средних, а именно:

сумму, характеризующую изменчивость, обусловленную исследуемым фактором:

;

сумму, характеризующую изменчивость внутри каждого объекта (остаточная изменчивость):

сумму, характеризующую общую изменчивость наблюдаемого признака:

При выполнении сделанных предположений о величинах справедливо равенство: Q=Q1+Q2. А оценки соответствующих дисперсий:

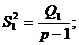
Критерий, используемый для проверки гипотезы H0, имеет вид:

При условии, что гипотеза H0 - верна, распределение критерия подчиняется закону Фишера (F-распределение) с (p-1) и (np-p) степенями свободы. Гипотеза отклоняется, если F>Fa, p-1,np-p, где Fa, p-1,np-p - табличное значение F-распределения, соответствующее уровню значимости a с (p-1) и (np-p) степенями свободы.

Б). Многофакторный дисперсионный анализ. В геологии нередки ситуации, в которых удается контролировать два и более факторов, предположительно управляющих исследуемой случайной величиной. Методы многофакторного дисперсионного анализа позволяют не только оценить влияние отдельных факторов, но и обнаружить (при определенных условиях) их взаимодействие.

Рассмотрим случай с двумя факторами (он может быть обобщен на большее число факторов) когда исходные данные можно представить в виде таблицы (случай с равными числами наблюдений в ячейках):

Общую модель можно записать в виде: yijm=m+ai+bj+gij+eijm, i=1,…,q; j=1,…,p; m=1,…,n. Нулевые гипотезы, утверждающие, что влияния фактора A и фактора B одинаковы, а взаимодействие между A и B отсутствует следующие:

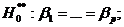
В реальных ситуациях нередко наблюдается невыполнение требований нормальности ошибок, некоррелированности результатов наблюдений и равенства дисперсий. Если нарушения значительны, то статистические решения, принимаемые на основе дисперсионного анализа, могут оказаться ошибочными. Поэтому необходима предварительная проверка соответствия исходных данных указанным требованиям. В некоторых случаях достичь такого соответствия удается с помощью некоторых преобразований исходных данных (например, логарифмирования). Труднее всего устраняется влияние стохастической зависимости наблюдений. Если устранить нарушение основных предположений не удается, то рекомендуется использовать непараметрический дисперсионный анализ.

В). Непараметрический дисперсионный анализ. Единственное требование, предъявляемое при использовании метода - непрерывность распределение исследуемой случайной величины. Устойчивость процедур дисперсионного анализа обеспечивается переходом от значений случайной величины к их рангам (при методе Краскла-Уэллиса) или нормальным меткам (метод Пури и Сена).

Однофакторный ранговый дисперсионный анализ Краскла-Уэллиса. Гипотеза H0 утверждает, что вычисленные средние, вычисленные по p выборкам, незначимо отличаются друг от друга. Процедура ее проверки сводится к следующему.

1. Все наблюдения объединяются в одну выборку объемом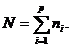

2. Производится ранжирование элементов этой выборки (от 0 до N, без учета совпадающих значений).

3. Вычисляется статистика:

где Ri - сумма рангов в i-ой выборке (i-ая градация фактора).

В условиях H0 величина H имеет c2-распределение с (p-1) степенями свободы. Дополнительное условие: ni > 5 "i.

Однофакторный ранговый дисперсионный анализ, опирающийся на медианный критерий Брауна и Муда.

1. Все выборки объединяются в одну.

2. Ищется медианное значение y.

3. Строится таблица:

Если влияние фактора несущественно, то можно ожидать, что все группы (выборки) будут иметь одну и ту же медиану, т. е. mi=ni/2 "i.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28