особенно при небольших n, будет несколько занижена по сравнению с σ2, что исправляется выражением:

.

Эта оценка является несмещенной.

Состоятельность. Пусть q*(x1),…, q*(x1,…,xn) - последовательность оценок полученных по выборкам объема k=1, 2, … ,n. Такую последовательность называют состоятельной, если

где e - сколь угодно малое заданное число. Это означает, что, начиная с некоторого объема выборки n, значения оценки практически не изменяется.

Эффективность. Оценка q*(x1,…,xn), обладающая минимальной дисперсией из всех возможных оценок, полученных по выборке объема n, называется эффективной:

Dq*(x1,…,xn)=min.

Такая оценка, если она не смещена, предпочтительнее любой другой, так как обеспечивает наиболее тесную группировку результатов около истинного значения, оцениваемого параметра q.

Достаточность. Пусть f(xi,θ) – плотность вероятности случайной величины в точке xi. Тогда для выборки объема n функция правдоподобия будет определена выражением:

Оценка называется достаточной оценкой неизвестного параметра θ*, если существует такая функция h(x1,…,xn), не зависящая от θ, для которой имеет место равенство:

Достаточная оценка содержит всю информацию, которую можно получить о неизвестном параметре по выборке объема n.

Для получения оценок часто используются метод моментов и метод максимального правдоподобия. В качестве примера рассмотрим метод поиска среднего значения q нормально распределенной случайной величины с известной дисперсией методом максимального правдоподобия.

Пусть плотность распределения случайной величины x:

).

В качестве функции правдоподобия выберем:

L(x, q)=ln(f(x, q)).

Тогда ее максимум найдем из условия

Глава II. Проверка статистических гипотез

§ 1. Особенности применения статистических критериев

Это некоторая вычислительная процедура, в результате которой можно подтвердить или опровергнуть какое-либо предположение. Она осуществляется с помощью некоторых случайных величин, называемых статистическими критериями. Так как каждый из критериев является случайной величиной, то он полностью характеризуется соответствующей функцией распределения при условии, что проверяемая гипотеза верна. Проиллюстрируем особенности применения статистических критериев (на примере проверки гипотезы о соответствии модели нормального распределения эмпирическим данным для выборок большого объема).

Проверка гипотезы осуществляется с помощью отношений оценок асимметрии (A=M(x-Mx)3/s3) и эксцесса (E=M(x-Mx)4/s4-3) и заключается в совместном выполнении двух предположений. Во-первых, в условиях близкого к нормальному распределению выборочных данных отношение v3/s3 (где v3 – оценка M(x-Mx)3, а s – оценка стандартного (среднего квадратического) отклонения s) должно представлять собой значение случайной величины, распределенной асимптотически нормально с математическим ожиданием, равным нулю, и дисперсией, равной единице. Во-вторых, в тех же условиях разность v4/s4-3 должна представлять собой значение аналогичной случайной величины, распределенной асимптотически нормально со средним равным нулю и дисперсией, равной единице.

Для примера рассмотрим лишь часть общей гипотезы о нормальности, а именно, только предположение о равенстве нулю среднего для отношения v3/s3. Этому предположению соответствует нулевая гипотеза:

H0: M(v3/s3)=0,

а в качестве альтернативы этому предположению можно использовать гипотезу:

H1: M(v3/s3)¹0

(двустороннее множество альтернатив), либо пару гипотез:

В результате проверки нулевой гипотезы может быть допущена ошибка, заключающаяся в принятии альтернативной гипотезы, хотя на самом деле верна нулевая гипотеза. Такая ошибка называется ошибкой первого рода. Наоборот, ложное принятие нулевой гипотезы, хотя она неверна, называется ошибкой второго рода. Для простоты изложения рассмотрим пример, в котором фигурирует одностороннее множество альтернатив вида:

Пусть j0(t) – функция плотности распределения v3/s3 в условиях нулевой гипотезы (Рис. 1). Функцию плотности распределения v3/s3 в условиях одной из альтернатив одностороннего множества обозначим через j1(t).

Задавая некоторое критическое значение D0, восставим из этой точки перпендикуляр, делящий плоскость рисунка на два множества: R0 и R1. Припишем областям R0 и R1 следующие свойства. Если при вычислении эмпирического значения v3/s3 мы получим величину, меньшую D0, т. е. значение окажется в области R0, то нулевую гипотезу следует принять. В противном случае, т. е. при попадании вычисленного значения v3/s3 в область R1, нулевая гипотеза должна быть отвергнута. Область R0 называется областью принятия нулевой гипотезы, а область R1 - областью отклонения нулевой гипотезы, или критической областью.

Как уже отмечалось, эти выводы, т. е. принятие или отклонение нулевой гипотезы, могут оказаться ошибочными. Какова же вероятность допустить ошибку при данном критическом значении D0 и сформулированном множестве альтернатив?

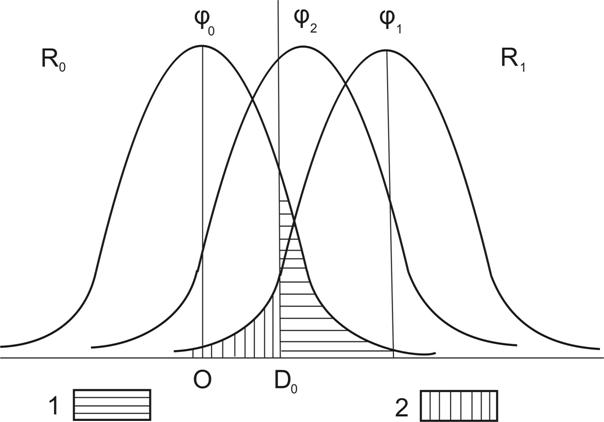
Рис. 1. Функции плотностей распределения v3/s3 в условиях нулевой и альтернативных гипотез. Ошибки первого и второго рода (для : 1 – вероятность ошибки первого рода, 2 – вероятность ошибки второго рода).

Вероятность ошибки первого рода, при заданных D0 и , отвечает области находящейся на рисунке под кривой j0(t) в области R1. Обозначив вероятность ошибки первого рода, соответствующую критическому значению D0, через a, выразим ее в рассматриваемом случае следующим образом:

.

Обозначим через b вероятность ошибки второго рода. При сформулированной альтернативе она равна:

.

Функция, заданная на множестве альтернатив:

,

называется функцией мощности критерия при заданном множестве альтернатив .

Рассмотрим более подробно соотношение a, b, 1-b. Нетрудно заметить, что a определяется значением D0. С равным основанием можно сказать, что величина D0 может быть определена через a. Дело в следующем. Зная функцию плотности распределения величины v3/s3 в условиях нулевой гипотезы, можно указать такое значение v3/s3, чтобы появление значений, больших по величине, чем выбранное, происходило с заданной малой вероятностью a. Это и есть D0. Вероятность a можно выбрать, в свою очередь, так, чтобы при единичном эксперименте (вычислении v3/s3) осуществление события v3/s3>D0 было бы практически невозможным. В этом случае вполне естественно считать, что данное значение v3/s3>D0 практически нельзя считать принадлежащим совокупности, которая характеризуется функцией j0(t), а следует отнести скорее к альтернативной совокупности, распределение которой подчиняется функции плотности j1(t). Таким образом, значение D0 устанавливается заранее и соответствует определенному заданному риску ошибочно отвергнуть верную нулевую гипотезу. Вероятность появления ошибки первого рода равна a и обычно называется уровнем значимости.

Уровень значимости и, следовательно, величина D0 определяют вероятность ошибки второго рода, т. е. b. Последняя, кроме того, зависит от альтернативы. Следует отметить, что для различных альтернатив ошибка второго рода и мощность критерия могут быть разными. Положим, что существует альтернатива , в условиях которой v3/s3 имеет распределение с функцией плотности j2(t). Нетрудно видеть, что при этой альтернативе значительно увеличилась вероятность ошибки второго рода. Ей соответствует площадь под кривой в области R0, т. е.:

.

Это означает, что мы в большом числе случаев ошибочно будем принимать ложную гипотезу. Иными словами, в значительном числе экспериментов мы не сможем отличить значения величины v3/s3, принадлежащие разным совокупностям: совокупности критерия в условиях нулевой гипотезы и в условиях альтернативы. Это можно назвать потерей чувствительности критерия к данной альтернативе.

Следовательно, падение мощности критерия влечет за собой уменьшение его чувствительности, т. е. снижает возможность различить действительно разные совокупности. Для одних и тех же выборочных данных, применяя при проверке одной и той же нулевой гипотезы различные критерии, обладающие разной мощностью при заданной альтернативе, можно получить сильно отличающиеся результаты. Поэтому мощность критерия является показателем его качества.

Существует класс критериев, которые обладают наибольшей мощностью при проверке определенной нулевой гипотезы по отношению ко всему множеству возможных альтернатив: класс "равномерно наиболее мощных критериев".

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28