![]()
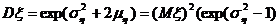 ,
,
т. е. в логарифмически нормальном распределении математическое ожидание и дисперсия зависимы. Если воспользоваться не натуральными логарифмами, а любыми другими, то структура вышеприведенных выражений не изменится.
Логнормальное распределение широко применяется в самых различных областях естествознания. показал, что логарифмически-нормальному распределению подчинены размеры частиц, образующихся при дроблении; на основании этой схемы предпринимались попытки привлечь логнормальный закон для описания гранулометрических характеристик кластических осадочных пород.
Большой объем работ был также проделан геологами по проверке согласия с логнормальным законом выборочных распределений содержаний редких и малых элементов в породах различного генезиса. Хотя во многих случаях аппроксимация логнормальным распределением вполне удовлетворительна, надлежащее теоретическое обоснование, ведущее именно к логнормальной модели, почти всегда отсутствует. Это не позволяет исследователю дать генетическую интерпретацию полученных таким путем вероятностных моделей. Тем не менее, если ограничиться задачей подбора достаточно приемлемой аппроксимации наблюдаемых в результате опыта асимметричных распределений (например, для более сжатого представления обширной выборочной информации или с целью более обоснованного применения некоторых статистических критериев и т. п.), то логнормальный закон нередко оказывается вполне подходящей моделью.
Распределение Стьюдента или t-распределение. Это распределение случайной величины t=x/h, где
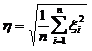 ,
,
а случайные величины x и x1,...,xn независимы и нормально распределены с параметрами 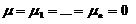 и
и ![]() .
.
Плотность распределения случайной величины t определяется формулой:
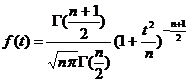 ,
,
где n - число степеней свободы, а G(x)=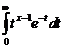 - гамма-функция. В частности: G(n+1)=n!, G
- гамма-функция. В частности: G(n+1)=n!, G![]() =
=![]() , G(x+1)=xG(x). Распределение Стьюдента унимодально и симметрично относительно x=0.
, G(x+1)=xG(x). Распределение Стьюдента унимодально и симметрично относительно x=0.
Моменты τ-распределения:
Mt2k-1=0; ![]() 2k<n;
2k<n;
Dt=¥, если n£2 и Dt=n/(n-2), если n>2.
Распределение Стьюдента – одно из наиболее важных специальных распределений в теории вероятностей и статистике. Оно табулировано и приведено в таблицах.
Распределение Стьюдента широко используется в геологии при проверке гипотез о средних значениях геологических характеристик. Квантили распределения Стьюдента используются при построении доверительных интервалов геологоразведочных параметров.
Распределение Фишера или F-распределение. Это распределение случайной величины ![]() , где x1 и x2 - независимые случайные величины, имеющие c2-распределение соответственно с m1 и m2 степенями свободы. Плотность вероятностей случайной величины h, имеющей распределения Фишера:
, где x1 и x2 - независимые случайные величины, имеющие c2-распределение соответственно с m1 и m2 степенями свободы. Плотность вероятностей случайной величины h, имеющей распределения Фишера:
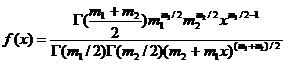
при x>0 и f(x)=0 при x£0.
Математическое ожидание и дисперсия случайной величины η
![]() ,
, ![]() >2;
>2;
![]() ,
, ![]() >4.
>4.
F-распределение табулировано и приведено в таблицах. Отметим, что отношение оценок дисперсии двух случайных величин, подчиняющихся нормальному закону, описывается F-распределением. Это обстоятельство определяет его широкое применение в дисперсионном анализе.
Распределение c2 (хи-квадрат). Это - распределение случайной величины c2, плотность вероятностей которой описывается формулой:
f(x)=![]()
при x>0 и f(x)=0 при x£0, где G(.) - гамма-функция; n - число степеней свободы. Математическое ожидание и дисперсию случайной величины c2 можно записать:
Mc2=n; Dc2=2n.
Распределение c2 табулировано и приведено в таблицах. Широкое применение c2-распределения в теории вероятностей и математической статистике определяется тем обстоятельством, что случайную величину c2 можно представить как сумму квадратов независимых случайных величин, имеющих одно и то же стандартное нормальное распределение (Mξi=0; Dξi=1; i=1,…,n):
§ 3. Основные понятия математической статистики
Математическая статистика - раздел математики, объектом которого является получение надежных выводов из статистических данных и выработка методов, с помощью которых эти выводы могут быть получены. Основная задача математической статистики - на основании одной или нескольких выборок сделать вывод обо всем содержимом той совокупности, из которой производится выбор. В геологических исследованиях наиболее широко используются следующие разделы математической статистики: оценка параметров распределения; проверка гипотез о некоторых хорошо изученных законах распределения; проверка статистических гипотез о равенстве или различии параметров распределения либо других статистических характеристик в двух или нескольких изучаемых совокупностей. При прогнозировании геологических характеристик широко используется аппарат корреляционного и регрессионного анализа.
Генеральная совокупность - математическая абстракция, используемая в математической статистике для описания совокупности объектов, которые подвергаются обследованиям с помощью случайного выбора ее представителей (случайного эксперимента).
В данном случае случайный эксперимент заключается в следующем. Пусть задано некоторое множество элементов. Мы наугад выбираем какой-нибудь элемент из этого множества, регистрируем какую-либо его характеристику и затем возвращаем его назад. При этом предполагается, что вероятности, быть выбранными, равны для всех элементов. Заданное множество - генеральная совокупность, а описанный процесс выбора - простой случайный выбор. Если мы интересуемся значениями регистрируемой характеристики (случайной величины), то генеральная совокупность - это множество всех ее значений, а последовательность наблюденных значений x1,x2,…,xn - случайная выборка (выборка с возвращением) из этой генеральной совокупности.
Выборка - множество наблюдаемых значений одномерной или многомерной случайной величины с некоторой функцией распределения. Выборка значений многомерной случайной величины (когда в эксперименте регистрируется p характеристик, где p > 1) может быть представлена как множество точек в p-мерном пространстве.
Частоты распределения - выборочные характеристики распределения (статистический аналог плотности вероятности распределения). Наблюдая частоты некоторого события для возрастающего числа испытаний, мы обнаружим, что эта частота стремится к постоянному значению (вероятности появления этого события).
Гистограмма - график частот распределения в последовательности независимых случайных экспериментов: по оси абсцисс откладываются значения случайной величины, а по оси ординат - частоты.
Выборочное среднее. Для одномерного распределения выборочное среднее равно:
![]()
![]() ;
;
для многомерного распределения - это вектор средних арифметических значений компонент наблюдаемых векторов.
Выборочная дисперсия. Для одномерного распределения выборочная дисперсия равна:
![]() =
=![]() ;
;
![]() - выборочное среднее квадратическое отклонение или выборочное стандартное отклонение.
- выборочное среднее квадратическое отклонение или выборочное стандартное отклонение.
Выборочная ковариацияслучайных величин x и y равна:
cov(x, y)=![]()
Число степеней свободы это ранг некоторой квадратичной формы, переменными в которой являются независимые нормально распределенные случайные величины. Сущность этого параметра заключается в том, что он отражает разницу между числом наблюдений в выборке и числом параметров, которые требуется оценить по выборочным данным (превышение числа наблюдений над числом оцениваемых параметров распределения). В этой связи можно отметить, что выборочная дисперсия имеет (n-1) степень свободы, т. к. одно из слагаемых автоматически выражается через остальные.
§ 4. Типы оценок и методы оценивания
Для одного и того же неизвестного параметра могут существовать различные варианты оценок. Чтобы обосновано подходить к той или иной из них необходимо рассмотреть критерии их качества. Важнейшие из них следующие.
Несмещенность. Пусть q - неизвестный оцениваемый параметр, q*(x1,…,xn) - оценка для q, а n - объем выборки. q*(x1,…,xn) - случайная величина. Если выполнено условие:
Mq*(x1,…,xn)=q,
то такая оценка называется несмещенной, т. е. не содержащей систематической ошибки.
Если требование несмещенности не выполняется, этот недостаток обычно бывает легко устраним путем введения соответствующей поправки. Так, например, математическое ожидание оценки дисперсии:

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |




