Математические методы моделирования параметров геологических процессов и явлений (стр. 24 )

Точный ранг матрицы сходства равен 3. Но если считать приближенно ранг равным 2, то будет учтено 99,77% суммарной информации. Таким образом, для приближенного описания состава 5 образцов горных пород необходимы 2 крайних члена, т. е. два линейно независимых вектора.

Матрица факторных нагрузок:

Столбцы матрицы факторных нагрузок - ортогональные собственные векторы матрицы сходства, умноженные на квадратные корни из соответствующих собственных чисел. Сумма квадратов элементов столбца равна соответствующему собственному числу (определяет вклад в дисперсию). Элементы любой строки матрицы - косинусы углов между вектор-строкой матрицы исходных данных и соответствующей факторной осью. Сумма квадратов элементов строки - общность.

Матрица значений факторов:

Элементы столбцов матрицы значений факторов отражают относительный вес каждой переменной в данном факторе. Эту матрицу можно использовать для определения положения в факторном пространстве объектов, которые отсутствовали в исходной матрице: a'=w'F, где F - матрица факторных значений, w' - нормализованный (длина=1) вектор нового объекта.

Вычислив матрицы факторных нагрузок и значений, переходим к поиску множества различных по составу крайних членов. Найденные факторы не удовлетворительны для этих целей. Одним из способов решения этой задачи является варимаксное вращение факторов. Этот метод заключается в нахождении такого ортогонального поворота факторных осей, при котором они максимально совпадают с наиболее удаленными друг от друга векторами в пространстве факторов. Это достигается путем максимизации дисперсии всех факторных нагрузок при условии сохранения ортогональности факторов.

Матрица варимаксных факторных нагрузок:

Матрица варимаксных значений факторов:

Косоугольные проекции. Объекты, характеризующиеся наибольшими различиями в составе, можно рассматривать в качестве крайних членов. В более сложных случаях, матрица варимаксных факторных нагрузок для поиска крайних членов может оказаться не совсем пригодна. Имбри описал процедуру, называемую косоугольным проектированием, которая поворачивает ортогональные варимаксные оси таким образом, чтобы они совпали с крайними по составу векторами-объектами. Получаемые факторы уже не ортогональны, но соответствуют реальным объектам, что в ряде ситуаций более выгодно. Эта процедура приводит к нахождению наиболее контрастных по составу вектор-строк матрицы данных, хотя единственного решения в некоторых случаях получить нельзя.

2. Метод главных координат.

Метод главных координат (термин введен Гувером) - один из методов Q-модификации факторного анализа, используемый при решении задач упорядочения данных. Следует отметить, что цели метда главных координат и Q-метода совпадают лишь частично. С точки зрения Q-метода Имбри графический анализ данных является лишь одной из целого ряда задач, в то время как для иетода главных координат такой анализ является главной целью.

Описание метода. Главные координаты можно считать аналогами главных компонент Q-метода, полученных по матрице связей особого вида. Основой процедуры является выделение первых k собственных чисел и собственных векторов матрицы связей порядка N´N, вычисленной по исходной матрице данных X (N - объектов и p - параметров):

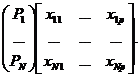
Обычно эти связи - те или иные меры расстояния между объектами. При этом следует отметить одно очень важное обстоятольство: переменные не обязательно все должны быть количественными, некоторые из них могут представлять собой тем или иным способом масштабированные качественные переменные, другие - альтернативные, т. е. переменные типа есть-нет, плюс-минус, нуль-один. Элементы матрицы сходства:

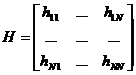
представляют собой коэффициенты связи между объектами (hmn - коэффициент связи между m-м и n-м объектами). Такую матрицу можно получить используя любую известную меру сходства или меру связи.

Расстояния между объектами. В МГК в ряде случаев, например при исследовании расстояний между объектами, используют диаграммы значений преобразованных переменных u1z1+…+upzp в проекциях на первый собственный вектор стандартизированных переменных (значения главных компонент). Расстояния между проекциями выборочных точек Qm и Qn (соответствующих точкам Pm и Pn) лишь приближенно соответствуют расстоянию между исходными выборочными точками. Евклидово расстояние между точками Pm и Pn в p-мерном пространстве задается: 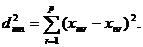Недостатками этой меры расстояния являются: она не учитывает взаимосвязи между переменными и она не инвариантна относительно единиц измерения переменных.

Обобщение понятия Q-модификации. До сих пор использовалось понятие расстояния в терминах R-метода главных компонент. Рассмотрим расширение этого понятия на Q-модификацию, введенное Гувером. Гувер показал, что если для любой пары объектов выборки определена мера их связи, или сходства, hmn, то можно найти такие координаты точек P1,…,PN относительно главных осей, что выполняется соотношение:

Если hmn - это мера сходства, то диагональные элементы матрицы H равны 1 (так как каждый объект имеет сходство с самим собой 1). В этих случаях квадрат расстояния между точками:

Если , где - обычное евклидово расстояние между объектами Pmи Pn, то hii=0 для всех i, поэтому 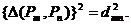N точек всегда содержится в пространстве размерности N-1, поэтому при использовании метода главных координат по крайней мере 1 собственное число должно быть равно нулю. Выполнение этого условия для евклидовых метрик обеспечивает преобразование к матрице H*:

,

где h.. - среднее по всем элементам H, а hm. и h. n - средние по строке и столбцу соответственно. Элемент есть квадрат расстояния от центра 0 до точки Pm, а элемент - произведение косинуса угла между векторами 0Pm и 0Pn на расстояния 0Pm и 0Pn. Если ранг матрицы H* равен r, то координаты точек P1,…,PN можно представить в виде матрицы A размерности N´r, столбцами которой являются собственные векторы матрицы H*, нормированные таким образом, что квадраты их длин равны собственным числам в порядке их уменьшения. Следовательно:

Обычно важно спроектировать точки в пространство малой размерности. Это можно сделать, используя только первые k столбцов матрицы A. Строки этой "урезанной" матрицы представляют собой координаты проекций точек P1,…,PN в наиболее близком к исходному подпространстве размерности k. Если полученная аппроксимация достаточно удовлетворительная, то расстояния между проекциями точек приблизительно те же, что и между точками. Другое свойство такой аппроксимации состоит в том, что проекции точек концентрируются вокруг начала координат, так как суммы элементов всех столбцов матрицы A равны нулю. Это свойство - следствие того, что сумма элементов любой строки и столбца H* равна нулю.

Отметим, что любое преобразование матрицы H влечет изменение расстояний между проекциями точек, а следовательно, и нарушение конфигурации множества объектов в пространстве главных координат. Особенно часто такие эффекты появляются, если матрица H строится по альтернативным данным "есть-нет". Если матрица H строится по отличной от евклидовой метрике, то возникают осложнения: матрица H* может иметь отрицательные собственные числа.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28