![]()
![]()
4. Для запасов полезного компонента единичного блока при аппроксимации нормальной моделью.
Группируем N полных пересечений в блоке произвольным образом в m групп по n пересечений в каждой группе: N ≈ m*n, (можно N = m*1, т. е. m=N) при соблюдении условия: m >> n.
Для каждой серии I = 1, 2, …, m в отдельности находят средневзвешенное содержание рудного компонента ![]() и среднее арифметическое значение мощности рудного тела
и среднее арифметическое значение мощности рудного тела ![]() :
:
![]() и
и ![]() ; i = 1, 2, …, m,
; i = 1, 2, …, m,
где Mt — полные пересечения (мощности рудного тела).
Каждое полное пересечение состоит из k (k ≥ 1) секционных проб с содержанием рудного компонента Cu и длиной секции lu = 1, 2, ..., k. Поэтому средневзвешенное содержание рудного компонента по каждому пересечению Ct и мощность по пересечению Mt, t = 1, 2, . . . , N определяются как:
![]()
![]()
![]()
где lu - длина секционной пробы.
Для каждой серии i = 1, 2, . . . , m в отдельности по общепринятой формуле подсчета запасов определяют оценки запасов рудного компонента ![]() :
:
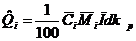 , (i = 1, 2, …, m),
, (i = 1, 2, …, m),
где П - площадь блока в плоскости блокировки запасов, м2; d - объемная масса руды, т/м3; kp - коэффициент рудоносности (часто принимаемый за единицу); ![]() - коэффициент для перехода от весовых процентов к тоннам металла.
- коэффициент для перехода от весовых процентов к тоннам металла.
В дальнейшем процедура построения интервальных оценок аналогична вышерассмотренному:
![]() (i= 1, 2, …, m);
(i= 1, 2, …, m);
![]()
![]()
![]()
![]()
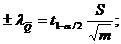
![]()
![]()
![]()
5. Для запасов полезного компонента единичного блока при аппроксимации логнормальной моделью, с учетом наличия ураганных сечений. Процедуры интервального оценивания аналогичны в этом случае пунктам 2, 3 и 11.
6. Для суммарных запасов полезного компонента группы блоков, рудных тел, участков месторождения. По каждому V-му блоку (V = 1, 2, …, k) имеется NV полных пересечений, в каждом из которых оценивается среднее взвешенное содержание рудного компонента Ct, t = 1, 2, . . . , NV, производятся замеры мощности mt, на геолого-маркшейдерских планах замеряются площади блоков ПV, V = 1, 2, . . . , k, определяются объемные массы руды dV, V = 1, 2, . . . , k по всем блокам, а также в случае необходимости коэффициенты рудоносности ![]() , V = 1, 2, . . . , k.
, V = 1, 2, . . . , k.
По каждому из k блоков в отдельности находят оценки запасов ![]() и их дисперсии
и их дисперсии ![]() (п. 4):
(п. 4):
![]()
![]()
Затем определяются: оценка суммарных запасов ![]() , ее дисперсия
, ее дисперсия ![]() стандартное отклонение
стандартное отклонение ![]() , точность суммарных запасов при заданной надежности
, точность суммарных запасов при заданной надежности ![]() :
:
![]()
![]()
![]()
![]()
Строятся интервальные оценки суммарных запасов:
![]()
![]()
7. Для суммарных запасов полезного компонента по сумме промышленных категорий (А + В + С1). Предположим, что по категории А разведано k1, по категории В – k2, а по категории С1 – k3 блоков. По каждому V-му блоку находят оценку запасов ![]() и оценку дисперсии
и оценку дисперсии ![]() (п. 4):
(п. 4):
![]() (категория A);
(категория A);
![]() (категория B);
(категория B);
![]() (категория C1).
(категория C1).
Находят оценки суммарных запасов и их дисперсий по категории ![]() , по категории
, по категории 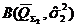 и категории
и категории 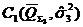 :
:
![]()
![]() где
где 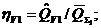
![]()
![]()
![]() где
где 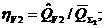
![]()
![]()
![]() где
где 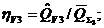
![]()
Строят интервальные оценки суммарных запасов для каждой промышленной категории в отдельности:
![]() где
где ![]()
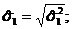
![]() где
где ![]()
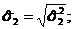
![]() где
где ![]()
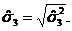
Находят оценку общих разведанных запасов по сумме категорий (A+B+C1) и ее дисперсию:
![]()
![]() где
где ![]()
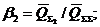
![]()
![]()
Строят доверительный интервал для разведанных запасов по сумме категорий (А + В + С1) при надежности 1-α (например, при 95% надежности):
![]() где
где ![]()
![]()
![]()
Величина 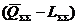 представляет собой минимально гарантированные запасы по сумме категорий (А + В+ С1).
представляет собой минимально гарантированные запасы по сумме категорий (А + В+ С1).
8. Для индикаторных отношений элементов, продуктивностей, показателей осевой, продольной, поперечной зональности геохимических аномалий, включая мультипликативные геохимические ореолы.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |




