Математические методы моделирования параметров геологических процессов и явлений (стр. 17 )

Возможность описания сложных поверхностей с помощью полиномов невысоких степеней определяется тем, что в сплайн-методе вся картируемая территория разбивается на относительно небольшие непересекающиеся участки - прямоугольники или треугольники, в вершинах которых размещены точки наблюдений. Аппроксимация полиномами осуществляется раздельно для каждого типа такого многоугольника. Обычно используются полином третьей степени - кубический сплайн. В этом случае возникает задача по обеспечению непрерывности функций в точках сочленения (гладкого склеивания).

Необходимые ограничения на искомые коэффициенты полиномов для реализации гладкого склеивания обеспечиваются системой равенств значений полиномов (для выполнения условия непрерывности), их первых и вторых частных производных в общих вершинах многоугольников. Алгоритмы нахождения коэффициентов в узлах правильной прямоугольной сети известны.

Если же данные расположены хаотически, то задача не имеет однозначного решения. Поэтому необходима дополнительная информация. Обычно предъявляется общее требование - максимальная плавность поверхности (минимальность средней кривизны).

2. Обособление локальной составляющей (выделение аномалий).

С этой задачей геолог сталкивается постоянно при геохимических поисках. В рамках данной задачи основная модель тренд-анализа приобретает вид:

z(x, y)=F(x, y)+L(x, y)+e(x, y),

где L(x, y) - локальная составляющая, а e(x, y) - случайные флуктуации признака z.

Здесь аномалии рассматриваются как полезный сигнал, а компоненты F(x, y) и e(x, y) соответственно как низкочастотный и высокочастотный шумы. Задача выделения аномалий сводится к подавлению этих шумов. Обычно частота L(x, y) заметно отличается от частоты региональной составляющей, но но близка к частотам e(x, y). Это обстоятельство не позволяет полностью отфильтровать случайные флуктуации, что приводит к выделению ложных аномалий. С другой стороны методы построения поверхности F(x, y) таковы, что вполне возможно поглощение ею компоненты L(x, y), что приводит к пропуску искомых аномалий. Положение может быть улучшено, если имеются хотя бы приближенные спектральные характеристики F(x, y) и e(x, y). Тогда удается построить полосчатый фильтр задерживающий мешающие частоты F(x, y) и e(x, y).

§ 3. Корреляционный анализ

Корреляционный анализ - это статистическое исследование стохастической зависимости между случайными величинами {Xi} и {Yj}. Задачи корреляционного анализа:

1 - оценка по выборочным данным коэффициентов парных корреляций;

2 - оценка по выборочным данным коэффициентов множественной корреляции;

3 - проверка значимости выборочных коэффициентов корреляции;

4 - оценка степени близости выявленной связи к линейной.

Если зависимость между Xi и Yj носит линейный характер, то удается охарактеризовать не только тесноту связи, но и ее направление. Связь называется прямой (положительной), если при увеличении (уменьшении) значений одной из переменных другая обладает устойчивой тенденцией к увеличению (уменьшению) своих значений. В этом случае коэффициент парной корреляции положителен. При обратном соотношении между переменными X и Y имеем дело с отрицательной корреляцией, что находит свое выражение в знаке коэффициента парной корреляции.

Парная корреляция.

1). Корреляция дихотомических признаков. Такая ситуация типична для тех случаев, когда исследователь фиксирует либо наличие, либо отсутствие некоторого определенного свойства. Пусть случайные величины X и Y принимают значения {x, x*} и {y, y*}, где x, y означает, что данные признаки фиксируются; x*,y* обозначает отсутствие этих признаков. В результате единичного наблюдения можно ожидать появление следующих сочетаний: (x, y), (x, y*), (x*,y) и (x*,y*). Выполнив N наблюдений, получим соответствующие частоты n11=n(x, y), n12=n(x, y*), n21=n(x*,y), n22=n(x*,y*). Для данных такого типа величина выборочного коэффициента связи, являющегося оценкой r (коэффициент связи в генеральной совокупности), отыскивается по формуле:

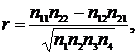
где n1=n11+n12; n2=n21+n22; n3=n11+n21; n4=n12+n22. Коэффициент r изменяется от -1 до 1, достигая крайних пределов в следующих случаях: n12=n21=0, тогда r=1; n11=n22=0, тогда r=-1.

Так как величина r, найденная по выборочным данным, испытывает случайные флуктуации, то вывод о зависимости X и Y не может быть сделан лишь на основании выполнения неравенства r¹0. Суждение о связи X и Y в генеральной совокупности будет обоснованным только после проверки гипотезы H0: r=0; при альтернативе H1: r¹0. Критерий, позволяющий выбрать одну из гипотез, имеет вид:

k=Nr2.

Распределение k в условиях нулевой гипотезы удовлетворительно описывается c2-распределением с одной степенью свободы. Следовательно, если 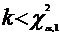, то принимается H0, а если , то H0 отклоняется и принимается H1. Выполнение последнего неравенства свидетельствует о зависимости случайных величин X и Y; теснота этой зависимости оценивается значением коэффициента r, а направление связи (прямая или обратная) - знаком r.

Имеется ряд других мер связи для работы с дихотомическими признаками. Наиболее употребительным является коэффициент связи Юла:

Коэффициент меняются от -1 до 1. Однако предельные значения могут быть достигнуты коэффициентом Q при обращении в нуль хотя бы одной из частот n12, n21 (Q = 1) или n11, n22 (Q = -1).

2). Корреляция для порядковых геологических данных. Это следующий, более высокий уровень описания свойств геологических объектов. Здесь производятся измерения с помощью порядковых шкал, что не только обеспечивает отнесение того или иного наблюдения к определенной категории (классу), но и позволяет упорядочить эти категории, т. е. расположить наблюдения x1,x2,… по возрастанию или убыванию степени проявленности (выраженности) измеряемого признака. Характерной особенностью порядковой шкалы является отсутствие сведений о величине различия между ее градациями. (Если удается упорядочить еще и разницу между классами, то такую шкалу называют порядково-метрической).

Пример порядковых шкал в геологических исследованиях - полуколичественные (приблизительная оценка содержания химических элементов: "очень много", "много", "мало", "следы", "не обнаружен" и т. п.) и приближенно-количественные (расстояния между соседними градациями точно не определимы) спектральные анализы. Но различия в степени детальности измерения содержаний химических элементов для этих двух типов анализа достаточно существенны. Это дает основания отдельно рассматривать меры связи для полуколичественных и приближенно-количественных данных. Полуколичественные данные называют категоризованными упорядоченными данными. Приближенно-количественные легко поддаются ранжированию, поэтому их называют ранговыми данными.

A). Категоризованные (упорядоченные) данные. Пусть значения случайных величин X и Y принимают в процессе испытания значения, соответственно {Ai| i-=1,…,r} и {Bj| j=1,…,s}. Законы распределения этих величин можно записать в следующем виде:

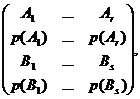
где и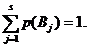

Их совместные (двумерные) распределения отражает матрица:

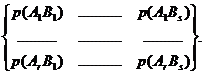
Элементами этой матрицы (таблицы сопряженности) являются вероятности совместного появления определенных значений случайных величин X и Y. Необходимым и достаточным условием независимости случайных величин X и Y является выполнение равенства: p(AiBj) = p(Ai) p(Bj). В качестве меры зависимости используют коэффициент сопряженности:

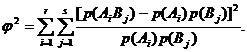
Свойства коэффициента сопряженности:

1)  0 £ j2 £1;

2)  j2 = 0 тогда и только тогда, когда X и Y независимы;

3)  j2 = 1, если X и Y связаны однозначной функциональной зависимостью.

Если число градаций (число отличающихся возможных значений X и Y) равно двум (r=2, s=2), то коэффициент сопряженности совпадает с квадратом коэффициента корреляции для дихотомических признаков.

Коэффициент сопряженности незаменим при исследовании зависимостей между такими свойствами геологических объектов, которые не поддаются упорядочению по самой природе явления. На практике коэффициент сопряженности применяют и для исследования связи между непрерывными случайными величинами, если отсутствуют сведения как о законе их распределения, так и о форме ожидаемой связи между ними. Коэффициент сопряженности позволяет оценить только силу связи между переменными. Для оценки силы и направления связи между X и Y, выборочные данные удобно представить в виде таблицы сопряженности:

В клетки таблицы вписаны частоты совместного появления значений случайных величин, принадлежащих определенным классам. Последняя строка и столбец отведены для суммарных частот (по столбцам и строкам соответственно, а ).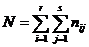

Выборочную меру связи вычисляют по формуле:

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28