Математические методы моделирования параметров геологических процессов и явлений (стр. 13 )

P(xg1≤xg2≤…≤xgm)=∫…∫∏dPgi(xgi), i=1, 2, …, m,

-∞ < xg1 ≤ … ≤ xgm < ∞,

где (xg1, xg2, …, xgm) – упорядоченные в неубывающем порядке значения признаков в реализации X. Предполагается, что все эти значения независимы.

Пусть имеем две реализации и , причем относительно первой известно, что она принадлежит образу A1. Тогда проверяем гипотезу H0 о том, что обе реализации имеют одинаковые распределения (т. е. X также относится к А1) против альтернативной гипотезы Н1 о различии этих распределений. При этом предполагается, что 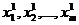и 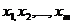- независимые случайные величины с функциями распределения соответственно Р (Х1) и f[Р (Х1) ].

Символически такую проверку гипотез можно записать так: проверяемая гипотеза Hо: Р = Р (Хх) при альтернативе H1: Р = f[P(X)].

Образуем из компонентов Х1 и X последовательность и обозначим и т. д. Тогда получим V(k)=(V1, V2, ..., Vk), k=1, 2, ..., 2m, где k - номер шага процесса. И пусть S(k) - вектор последовательных рангов для V(k), a:

- последовательное отношение вероятностей (на каждом шаге).

Если Hо истинна, то для любого S из S(k):

Таким образом, найден знаменатель в выражении для λk. Теперь для нахождения числителя в том же выражении достаточно заметить, что:

и

P(V1≤V2≤…≤Vk|H1)=∫…∫∏dfu[P(Vu)] (u=1, 2, …,k), где

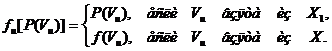
Полученные на каждом шаге значения λk сравниваются с двумя останавливающими границами и в случае выхода из этих границ принимается соответствующая гипотеза Hо или H1. Если λk не выходит за границы на данном k-м шаге, то процесс продолжается, k увеличивается на единицу и вычисляется λk+1, и т. д.

Описанный метод применим, когда в эталоне имеются представители только одного образа, и распознавание заключается в том, чтобы вынести решение, относится ли предъявляемая для распознавания реализация к этому образу или нет.

Вопрос выбора вида функции f в альтернативе может быть решен различным способом, одним из которых являются альтернативы Лемана. Альтернативы Лемана имеют вид f[Р(X)] = Pr(X), r>0.

В случае допустимости альтернатив Лемана для последовательного отношения правдоподобия получим:

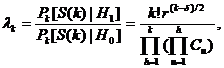где

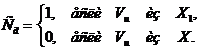
λk сравнивается с парой останавливающих границ, и как только происходит их пересечение, процесс останавливается и принимается соответствующее решение.

§ 2. Дискриминантный анализ

Решение задач классификационного отнесения изучаемых объектов к одной из заданных групп по комплексу признаков называется дискриминантным анализом. Методы дискриминантного анализа требуют только количественных данных. В основе дискриминантного анализа лежит хорошо развитая математическая теория, что позволяет учитывать риск, связанный с принятием ошибочных решений. Формально задача дискриминантного анализа сводится к следующему.

Пусть A1,…,Ak - k множеств объектов. Для простоты ограничимся случаем k=2. Множеству A1 поставим в соответствие m-мерную случайную величину x={x1,…,xm}, а множеству A2 - случайную величину h={h1,…,hm}. При этом известно, что некоторые параметры q1 и q2 для x и h - различны. Обычно в качестве таких параметров выбираются многомерные средние. Но могут быть выбраны и другие характеристики, например - ковариационные матрицы. Пусть из каждой A1 и A2 совокупности взяты выборки X и Y объемом n1 и n2 соответственно. По этим выборочным данным требуется построить решающее правило D, которое бы позволяло относить объекты из третьей совокупности A, представляющей собой смесь объектов из A1 и A2, к A1 или A2. Обозначим результаты m-мерных наблюдений из совокупности A, которая требует распознавания, через Z={zi}. Тогда наше решающее правило должно заключаться в том, что рассматриваемое наблюдение zi относится к совокупности A1, если оно характеризуется определенным множеством значений Z1, и к совокупности A2 при других значениях. Это условие приводит к тому, что все m-мерное пространство, будет разделено на две области R1 и R2, причем если результат наблюдения попадет в R1, то мы принимаем решение о его принадлежности к группе A1, а если он попадет в R2, то относим его к совокупности A2.

Оба решения не исключают появления ошибок, которые заключаются в следующем. Решение о принадлежности классифицируемого объекта aÎA к A1, т. е. aÎA1, ошибочно и он в действительности принадлежит к A2, т. е. aÎA2. Вторая возможная ошибка заключается в том, что принимается решение aÎA2, тогда как в действительности aÎA1. Каждой из этих ошибок можно приписать соответствующую цену, так как их появление нередко приводит к тем или иным потерям. Например, ошибочное отнесение объекта к перспективно рудоносным, тогда как в действительности он бесперспективен, приведет к потерям, связанным с безрезультативным проведением поисковых работ на этом объекте. А ошибочное отнесение перспективного объекта к бесперспективным приведет к потере месторождения, которое стоит обычно дороже, чем затраты на поисковые работы. Обозначим стоимости этих потерь соответственно через C(A1|A2) и C(A2|A1).

Таблица ошибок и их стоимостей:

Допустим, что в выборке, которую нужно подвергнуть разделению на объекты, принадлежащие совокупностям A1 и A2, эти объекты смешаны в определенном соотношении, и доля объектов aÎA1 равна q1, а объектов aÎA1 равна q2 (q1+q2=1). Тогда величину q1 можно рассматривать как вероятность события, заключающегося в том, что взятый наудачу из изучаемой смешанной совокупности объект будет принадлежать к A1. Аналогично интерпретируется и вероятность q2. Можно считать, что вероятностные свойства совокупностей A1 и A2 описываются плотностями f1(X) и f2(Y). Таким образом, если область m-мерного пространства (область значений X и Y) разделена на две непересекающиеся области R1 и R2, то вероятности появления ошибочных решений будут определены следующим образом:

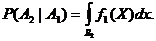
Теперь можно охарактеризовать потери, связанные с неправильной классификацией по следующей формуле:

W=C(A1|A2)P(A1|A2)q2+C(A2|A1)P(A2|A1)q1.

Это выражение представляет собой математическое ожидание потерь классификации или средние потери. Таким образом, области принятия решений R1 и R2 нужно выбрать так, чтобы потери W были по возможности меньше. Метод, который обеспечивает минимум W при заданных q1 и q2, называется методом Байеса.

Способ построения решающего правила D заключается в том, что R1 и R2 выбираются следующим образом:

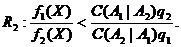
Обозначим: Предположим, что f1(X) и f2(Y) являются m-мерными нормальными плотностями с параметрами соответственно m1, S и m2, S. Т. е. вводим условие равенства ковариационных матриц распределений. Тогда область R1 можно определить с помощью неравенства:

После преобразований получаем: R1:

XS-1(m1-m2)’-1/2(m1+m2)S-1(m1-m2)’ ³ ln k.

Обычно в реальных геологических ситуациях нет никаких данных, позволяющих судить о вероятностях q1 и q2, а нередко и о ценах потерь C(A2/A1) и C(A2/A1). В таких ситуациях ничего не остается делать, как допустить, что C(A2/A1)=C(A2/A1) и q1=q2. Тогда ln(k)=0 и R1 определяется неравенством:

Если ковариационные матрицы неизвестны и оцениваются по выборке, то вместо S берется матрица S: где S1 и S2 - оценки ковариационных матриц. В этой ситуации бывает полезно применять квадратичное решающее правило:

§ 3. Многогрупповой дискриминантный анализ

Это обобщение процедуры дискриминантного анализа, связанной с разбиением на две группы. Введем следующие обозначения: xijk - i-ая переменная на j-ом объекте внутри группы k; nk - число объектов группы k; g - число групп, на которые классифицируются наблюдения; 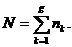Среднее i-ой переменной в k-ой группе: Общее среднее:

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28