где Akl - алгебраическое дополнение для элемента rkl матрицы R, т. е. определитель матрицы размерности m-1, которая получается, если в R вычеркнуть k-ю строку и l-й столбец, умноженный на (-1)k+l. Величина частного коэффициента корреляции меняется в пределах от -1 до 1.
В геологии, возможности которой в области активного эксперимента весьма ограничены, частная корреляция является одним из эффективных методов исследования взаимоотношения между компонентами сложных природных систем и параметрами внешней среды. Выборочный частный коэффициент корреляции есть оценка rij. q по выборочным данным частного коэффициента корреляции случайных величин xi и xj при фиксированных m-2 величинах {xl: l=1,…,m; l¹i; l¹j} следующего вида:
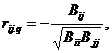
где Bij - алгебраическое дополнение выборочной корреляционной матрицы {rij} для совокупности случайных величин {xj: j=1,…,m}, соответствующее элементу rij.
Распределение rij. q, построенное по n наблюдениям, совпадает с распределением выборочного коэффициента парной корреляции [Стьюдент с числом (n-2) и Фишер с числом (1,n-2) или (n-2,n-2)] с уменьшением числа степеней свободы на m-2. Поэтому проверка значимости выборочного коэффициента частной корреляции проводится аналогичным образом.
6). Множественная корреляция.
Коэффициент множественной корреляции - мера линейной зависимости случайной величины xk от совокупности случайных величин {xl : l=1,…,m; l¹k}. Коэффициент множественной корреляции определяется формулой:
где |R| - определитель корреляционной матрицы R, имеющей размерность m*m; Akk - алгебраическое дополнение для элемента rkk матрицы R, т. е. определитель матрицы размерности m-1, которая получается, если в R вычеркнуть k-ю строку и k-й столбец.
Свойства коэффициента множественной корреляции:
1) 
2) 
Û 
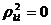"l; (rkl - парный коэффициент корреляции);
3) 
, если xk является строго линейной комбинацией совокупности случайных величин {xl : l=1,…,m; l¹k}.
Имеет место соотношение: 
следовательно, равенство коэффициента множественной корреляции единице выполняется всегда, когда значение хотя бы одного из парных коэффициентов корреляции с первым индексом k равно 1.
Множественная корреляция широко применяется в геологических исследованиях, например, при прогнозировании таких геологических признаков, измерения которых либо затруднительно по техническим причинам, либо невыгодны по экономическим соображениям.
Выборочным коэффициентом множественной корреляции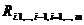 
между случайной величиной xi и набором x1,…,xi-1,xi+1,…,xm называется величина:
где Cii - диагональный элемент матрицы, обратной для матрицы выборочных коэффициентов корреляции.
Для проверки статистической гипотезы H0 о равенстве нулю коэффициента множественной корреляции:
при множестве альтернатив:
вычисляется величина:
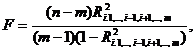
имеющая в условиях нулевой гипотезы F-распределение с m-1 и n-m степенями свободы.
При уровне значимости a по таблицам F-распределения находят 
критическое значение F-распределения с m-1 и n-m степенями свободы. Если F > Fa, m-1,n-m, то гипотеза H0 отклоняется, в противном случае - принимается как подтвердившаяся.
7. Каноническая корреляция.
Она служит для измерения силы связи между двумя множествами случайных величин.
Пусть X(1)={Xi, i=1,…,k}, X(2)={Xj, j=k+1,…,k+l}, X(1)ÇX(2)¹Æ, X=X(1)ÈX(2). Положим p1=k, p2=l, p=k+l и условимся, что p1£p2. Корреляционную матрицу размерности p*p разобьем на блоки: R11 - матрица p1*p1 парных коэффициентов корреляции между элементами подмножества X(1); R22 - аналогичная матрица p1*p2, относящаяся к подмножеству X(2); R12= T(R21) - матрицы размерностью p1*p2 и p2*p1. Тогда:
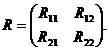
Нулевую гипотезу, предполагающую отсутствие линейной связи между подмножествами случайных величин X(1) и X(2), запишем:
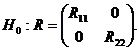
Нулевая гипотеза противопоставляется гипотезе H1, утверждающей, что подмножества случайных величин X(1) и X(2) не являются независимыми. Выбор между гипотезами H0 и H1 осуществляется на основе коэффициентов канонической корреляции, оценки которых (v1,…,vp-1ÎV) определяются как ненулевые корни уравнения:
где R11, R22, R21, R12 - блоки выборочной корреляционной матрицы R.
Суть канонической корреляции заключается в отыскании таких линейных комбинаций величин, составляющих подмножества X(1) и X(2), которые дают максимальную корреляцию U1. Затем в каждом из подмножеств находим новые линейные комбинации, опять же удовлетворяющие условию максимальной корреляции U2. При этом U1³U2, а линейные комбинации, полученные при нахождении U1 и U2, ортогональны, т. е. некоррелированы. Можно сказать, что первая линейная комбинация соответствует наиболее мощному фактору, общему для обоих подмножеств, тогда как вторая и последующие комбинации (всего их p1, если p1£p2) учитывают все более слабеющие попарно некоррелированные факторы. В результате получаем следующий ряд коэффициентов канонической корреляции: 
Принятие решения относительно гипотезы H0 опирается на критерий:
где N - объем p-мерной выборки, на основе которой формировалась матрица R.
При условии, что нулевая гипотеза верна, величина критерия I имеет c2-распределение. Нуль-гипотеза отвергается при уровне значимости a, если вычисленное значение I превысит предельно допустимое значение 
, выбираемое из таблицы. Число степеней свободы f регулируется объемами подмножеств X(1) и X(2) и составляет p1*p2. Следовательно, при 
коррелируемые подмножества случайных величин считаются зависимыми.
§ 4. Регрессионный анализ
Регрессионный анализ - совокупность статистических методов, ориентированных на исследование стохастической зависимости одномерной переменной Y от набора других переменных (X1,…,Xp). Его основными задачами являются:
1 - установление формы зависимости Y от (X1,…,Xp);
2 - определение вида уравнения регрессии;
3 - прогнозирование значений результирующей (зависимой) переменной Y, носящей названия отклика по известным значениям (независимых) переменных (X1,…,Xp), которые называются регрессорами.
Линейная регрессия. Основное уравнение регрессионного анализа имеет вид:
Yj=b1C1j+…+bpCpj+ej.
Здесь {Yj} - значения зависимой переменной; {Xij} - значения независимых переменных; {ej} - случайные отклонения (их появление чаще всего связывают с действием факторов, не учтенных измерениями независимых переменных); {bi} - неизвестные коэффициенты регрессии, оценки которых {bi}отыскиваются по выборочным данным.
Традиционный регрессионный анализ опирается на следующие допущения:
1 - Mej=0; Dej=s2<¥ для всех j;
2 - cov(ei, ej)=0 (i¹j);
3 - ранг матрицы X (исходных данных) равен p;
4 - значения Y достаточно однородны (извлечены из совокупности с распределением близким к нормальному);
5 - измерения переменных выполнены без существенных ошибок.
Различают линейную и нелинейную регрессию. При этом выделяются следующие классы:
1 - регрессии, линейные по X и по b:
Yj=b1C1j+…+bpCpj+ej;
2 - регрессии, линейные по b и нелинейные по X, например:
3 - регрессии, нелинейные по b, например:
Для регрессий линейных по X и b или только по b, вычисления оценок b неизвестных коэффициентов b производится методом наименьших квадратов. В основе этого метода лежит требование минимизации суммы квадратов отклонений эмпирических значений Y от значений Y*, вычисляемых по уравнению регрессии:
Этот же метод можно использовать и для регрессий, нелинейных по b, если удается подобрать подходящее преобразование к линейному виду. Например, для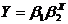 
применим преобразование logY=logb1 + X*logb2 и получим линейную зависимость.
Кроме того, обычно вводят фиктивную переменную X0, такую, что X0j = 1 для всех j. Это позволяет вместе с коэффициентами b1,…,bp вычислять и b0 - постоянную регрессии, сдвигающую поверхность регрессии в область скопления точек {yj, xij}.
Отыскав (b0,b1,…,bp) (в матричной форме: b=(X'X)-1X'Y), можно составить уравнение регрессии:
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
