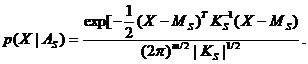
Тогда разделяющей будет:

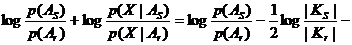
В случае равенства матриц ковариаций KS=Kr=K разделяющая граница принимает вид гиперплоскости:

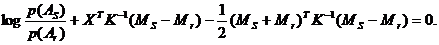
Модификациями метода распознавания на основе правила Байеса являются следующие:

1) метод заданного превышения максимальной вероятности гипотезы по отношению к ближайшей к ней. D* = Ds, если:

где р(As)р(X|As) - максимальное значение для р(Ar)p(X|Аr) по всем r; р(Аr)р(X|Аr) - ближайшее к максимальному значению того же выражения; С - константа, зависящая от требуемой надежности распознавания;

2) метод превышения максимальной вероятности гипотезы над суммарной вероятностью всех остальных гипотез. D* = Ds, если:

Критерий Вальда. Задача распознавания может быть решена не полным набором признаков, а некоторым его подмножеством. Рациональное соотношение между ложным распознаванием и числом использованных при этом признаков дает возможность добавлять признаки последовательно до тех пор, пока не будет достигнута требуемая точность распознавания.

В подобной процедуре становится существенным, в какой последовательности добавляются признаки. Понятно, что признаки следует расположить в такой последовательности, чтобы получить решение как можно скорее. Однако задача подобного упорядочивания признаков является самостоятельной задачей.

Пусть задано два класса А1 и А2. Рассмотрим последовательный процесс добавления признаков. На i-м шаге процесса, т. е. после измерения i-го признака, вычисляется последовательное отношение правдоподобия:

где pi(X|As) - i-мерная функция условной плотности вероятности для образа As (S = 1, 2). После этого λi сравнивается с двумя останавливающими границами (порогами) В1 и В2, и если λi≥B1, то принимается решение XÎA1, если λi≤B2,то принимается ХÎA2. В случае, если В2 < λi < B1, то добавляется следующий признак и производится (i+1)-й шаг. В качестве В1 и В2 выбраны выражения:

где lSr - вероятность принятия гипотезы XÎAS, когда в действительности истинна гипотеза XÎAr, S,r = 1, 2.

Можно доказать, что при заданных l12 и l21 не существует другой процедуры, которая обладала бы меньшими значениями вероятностей ошибок или среднего числа и давала бы выигрыш в среднем числе признаков по сравнению с последовательной процедурой классификации.

Пусть х1, х2, ... - независимые измерения признаков реализации X с одномерной нормальной функцией плотности р(xi|Aj), s = 1, 2; j = 1, 2, …, со средним значением m1 и дисперсией σ2. Тогда на первом шаге выбрано x1 и вычисляется:

Значение log(λ1) сравнивается с log(B1) и log(B2). Если 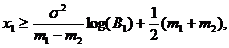то XÎA1,

и если

то добавляется x2 и т. д. На i-м шаге:

Если то XÎA1,

а если то XÎA2,

и если

то берется xi+1 и т. д.

Обобщенный критерий Вальда. Применяется для случая, когда число образов превышает два.

В этом случае на каждом i-м шаге для каждого 5-го образа вы­числяется обобщенное последовательное отношение правдоподобия:

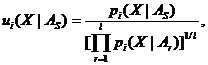S=1, 2, …, l.

Затем ui(X|As) сравнивается с останавливающей границей для S-го образа В(As), и если:

ui(X|As) < B(AS), S=1, 2, …, l,

то образ As из дальнейших операций исключается. После исключения S-го образа составляется новый набор последовательных отношений вероятностей.

Так продолжается до тех пор, пока не останется единственный образ, с которым и отождествляется X. В качестве останавливающих границ принимается выражение:

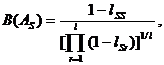S=1, 2, …, l.

Для случая двух образов обобщенный критерий Вальда эквивалентен последовательному критерию отношения правдоподобия Вальда и поэтому оптимален. Сохраняется ли оптимальность при l > 2, не доказано.

Усеченный критерий Вальда. При реализации последовательного критерия отношения правдоподобия или обобщенного критерия Вальда возможны два нежелательных случая:

1) алгоритмы могут потребовать слишком большого числа признаков;

2) среднее число признаков может стать очень большим, если величины lSr выбраны слишком малыми.

В этих случаях следует прервать последовательную процедуру на m-м шаге, и если до этих пор решение не было получено, то принимают решение XÎA1, если λm ≤ 1, или решение XÎA2, если λm > 1.

Для обобщенного последовательного критерия отношения правдоподобия Вальда процедура усечения проводится аналогично.

Модифицированный критерий Вальда. В рассмотренных выше критериях Вальда и обобщенном последовательном критерии отношения правдоподобия вероятности появления ошибок lSr задавались заранее. При этом число признаков, необходимое для принятия решения, является случайной величиной, зависящей от lSr, и может принимать любое значение. Вместе с тем желательно использовать алгоритм, который за конечное и заданное исследователем число шагов получит окончательное решение. Такими алгоритмами являются рассмотренные алгоритмы с усечением. К сожалению, алгоритмы с усечением являются алгоритмами с принудительной остановкой процесса, когда переход от продолжения к окончанию происходит скачкообразно. Чтобы сгладить скачок, может быть применена процедура с меняющимися от шага к шагу останавливающими границами.

Выберем невозрастающую функцию g1(x) и неубывающую функцию g2(х). Метод заключается в последовательной проверке неравенства:

при i=1, 2, … .

Если , то принимается решение XÎA1, если 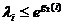, то XÎA2.

Положим:

где 0<r1, r2≤1, a>0, b>0.

В этом случае процесс закончится после m-го шага, так как в этом случае g1(m)=g2(m)=0, и неравенство 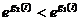, являющееся необходимым условием продолжения процесса, не выполняется.

Пусть x1, x2, … - независимые признаки с одномерной нормальной функцией плотности p(xi|AS), S=1, 2, … , со средними значениями mi и дисперсией σ2.

Тогда, вычислив:

получим следующую процедуру.

Если:

то XÎA1, а если:

то XÎA2, в противном случае, т. е. если:

добавляют (i+1)-й признак и делают (i+1)-й шаг вычислений. Если границы g1(i) и g2(i) заданы так же, как и раньше, то процесс закончится не позднее m-го шага.

Модифицированный обобщенный критерий Вальда. Как и раньше, для каждого S-ro образа на i-м шаге вычисляется обобщенное последовательное отношение вероятностей:

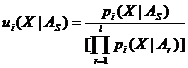
и сравнивается с останавливающими границами gS(i), где индекс S означает принадлежность к S-му образу.

Если ui(X|AS)<gS(i), то AS отбрасывается и в дальнейших вычислениях не участвует.

Такое отбрасывание производится до тех пор, пока не останется только один образ. Тогда к этому образу и относят исследуемую реализацию x.

В качестве порогов берут:

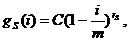S=1, 2, …, m; C>0, 0<rS≤1.

В описанных трех модифицированных алгоритмах можно выразить вероятности ошибок lij и среднее число измерений признаков, необходимое для принятия решения (это число равно числу шагов), через известные величины m, lSr, a, b, c, r1, r2. Оптимальность выбора параметров a, b, c, r1, r2, rS не исследовалась.

Последовательные ранги. Последовательным рангом значения признака xi реализации X=(x1, x2, …,xi, …, xm) называется число, равное Si, если xi является Si-й наименьшей величиной в этом множестве, i=1, 2, …, m.

Например, последовательный x1 всегда равен 1, последовательный ранг x2 равен 1 или 2, в зависимости от того, x2<x1 или x2>x1 и т. д.

Каждой реализации x будет соответствовать вектор последовательных рангов S(m)=(S1, S2, …, Sm). Поскольку между порядком расположения признаков и векторами последовательных рангов существует взаимнооднозначное соответствие, то в качестве функции распределения последних может быть взята следующая функция:

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28