Плотность распределения вероятностей - функция f(x), определяет вероятность того, что случайная величина x примет значение, принадлежащее интервалу (x, x+Dx). Связь между f(x) и F(x) выражается формулой: F(x)=![]() . Плотность распределения позволяет компактно и предельно полно описать вероятностные свойства исследуемой случайной величины.
. Плотность распределения позволяет компактно и предельно полно описать вероятностные свойства исследуемой случайной величины.
Математическое ожидание – M(ξ). В геологических исследованиях, опирающихся на вероятностные модели, математическое ожидание является важнейшим показателем, характеризующим среднее значение случайной величины:
M(ξ)=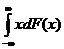 =
=![]() .
.
Квантиль порядка µ одномерного распределения F(x). Это значение xµ случайной величины x, для которого P{x<xµ}=F(xµ)=µ.
Медиана - Me(ξ). Величина, для которой имеет место: P(ξ<Me(ξ))=P(ξ>Me(ξ))=0.5. Это квантиль порядка 0.5. Таким образом, в результате случайного эксперимента величина ξ может с одинаковой вероятностью либо превысить медианное значение, либо оказаться ниже его. Медианное значение используется как характеристика положения случайной величины на числовой оси.
В случае нормального распределения медиана совпадает со средним значением M(ξ), а в случае логнормального имеет вид:
Me(ξ)=eμ,
где μ=M ln ξ. Медиана играет важную роль в непараметрической статистике.
Дисперсия – D(ξ). Она определяет меру «разброса» или рассеивания значений случайной величины ξ относительно математического ожидания ![]() . Дисперсия определяется следующим образом:
. Дисперсия определяется следующим образом:
D(ξ)=s2=M(ξ-Mξ)2=Mξ2-(Mξ)2.
Величина ![]() называется стандартным (средним квадратическим) отклонением.
называется стандартным (средним квадратическим) отклонением.
В геологических исследованиях, опирающихся на вероятностные модели, дисперсия является основным показателем, характеризующим изменчивость измеряемых свойств природных объектов. Дисперсия вместе с математическим ожиданием служит не только средством более сжатого представления количественной геологической информации, но и имеет важное самостоятельное значение. Дисперсия широко используется, например, в исследованиях, направленных на выяснение некоторых существенных особенностей геологических объектов.
Ковариация случайных величин ξ и η – cov(ξ,η). Широко используется при исследовании связи между двумя случайными величинами: x и h. Определяется следующим образом:
cov(ξ,η)=M((ξ-Mξ)(η-Mη)).
Ковариационная матрица - многомерный аналог дисперсии одномерной случайной величины. Характеризует рассеивание значений и зависимости между случайными величинами m-мерной совокупности x=(x1,...,xm). Ковариационная матрица m-мерной случайной величины x имеет вид:
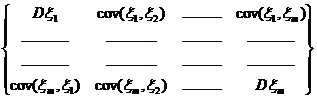
Мода – Mo(ξ). Мода - наиболее вероятное значение случайной величины (в дискретных распределениях) и значение, при котором плотность вероятности достигает максимума (для непрерывных величин). Если максимум один, то распределение называется одномодальным, если максимумов несколько - полимодальным.
Мода, как и математическое ожидание и медиана, является одной из характеристик положения случайной величины на числовой оси. Для симметричных одномодальных распределений эти параметры совпадают. В геологии полимодальность распределения обычно трактуется как следствие неоднородности исследуемого объекта. В случае нормального распределения мода совпадает с математическим ожиданием случайной величины, а в случае логнормального:
![]()
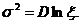
Показатель асимметрии. Это числовая характеристика степени асимметричности ("скошенности") кривой плотности распределения вероятностей случайной величины:
![]() .
.
Если g1>0, то говорят, что распределение обладает положительной асимметрией, если g1<0, то отрицательной асимметрией. В первом случае длинная часть («хвост») расположена справа, а во втором случае слева от моды. Если кривая плотности распределения симметричная, то g1=0.
В геологических исследованиях, использующих вероятностные методы, положение асимметричных распределений исследуемых геологических признаков (содержаний химических элементов и др.) довольно часто пытаются связать с особенностями генезиса природных объектов.
Эксцесс. Эксцесс это числовая характеристика кривой плотности вероятностей, отражающая степень ее "крутости", т. е. островершинности или плосковершинности. Для распределений, обладающих чрезмерно острой вершиной, характерна приуроченность подавляющего большинства значений случайной величины ξ к узкой области, примыкающей к моде. Плосковершинные распределения, наоборот, характеризуются «размазанностью» случайной величины ξ по всему интервалу ее возможных значений.
Эксцесс нормального распределения обычно рассматривается как эталон, с которым сравниваются эксцессы других теоретических распределений. Для нормального распределения величина M(ξ-Mξ)4/σ4 равна трем, поэтому формула, определяющая значение показателя эксцесса, имеет вид:
![]() .
.
Таким образом, коэффициент эксцесса в условиях нормального распределения принимает нулевое значение.
§ 2. Некоторые важнейшие типы распределений
Нормальное (гауссовское) распределение. Нормальное распределение – распределение случайной величины ξ, характеризующееся плотностью вероятностей типа:
![]() exp(-
exp(-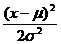 ),
),
где m - математическое ожидание (среднее); s2 - дисперсия случайной величины x. Параметры m и s2 однозначно характеризуют положение и форму кривой плотности распределения. Заменив x ее центрированным и нормированным аналогом ![]() , получим функцию стандартного нормального распределения Ф с параметрами μ’=0 и σ’=1:
, получим функцию стандартного нормального распределения Ф с параметрами μ’=0 и σ’=1:
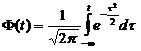 , где
, где 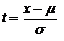 .
.
Значения этой функции, а также функции:
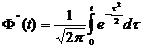 =
=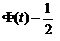 ,
,
связанной соотношением Ф(t)=0.5+Ф*(t), табулированы и приведены в таблицах.
При достаточно широких предположениях распределение суммы случайных величин с ростом числа слагаемых очень быстро приближается к нормальному закону.
Важность нормального распределения в естественнонаучных приложениях определяется тем, что распределения значений многих (но не всех) количественно измеряемых свойств природных объектов вполне удовлетворительно аппроксимируются нормальным законом. В связи с этим нормальный закон часто принимается в качестве вероятностной модели исследуемого явления, что, вообще говоря, может привести к ошибочным выводам, так как согласие результатов наблюдений с тем или иным законом распределения отнюдь не доказывает единственность именно этой модели. С содержательных позиций, особенно если решаются задачи генетического плана, наиболее ценны такие вероятностные модели (распределения), которые выбираются с учетом теоретических предпосылок, характеризующих физическую природу изучаемого явления.
В геологии стало традицией проверять согласованность выборочных распределений с нормальным законом. Многочисленные исследования, проведенные в этом направлении, показали, что существенное уклонение от нормального закона встречается чаще, чем это предполагалось ранее. Наиболее вероятная причина анормальности распределения геологических характеристик заключается, скорее всего, в невыполнении требований центральной предельной теоремы - равномерной малости и независимости факторов, генерирующих исследуемую случайную величину.
Многомерное нормальное распределение. Это распределение случайной величины ξ=( ξ1,...,ξn) с плотностью вида:
p(x1,…,xn)=(2p)![]() çSç
çSç![]() exp{(x-a)S
exp{(x-a)S![]() (x-a)'},
(x-a)'},
где S - ковариационная матрица, a - вектор математического ожидания (средних).
В качестве примера аппроксимации многомерным нормальным распределением может служить распределение петрогенных компонент по данным силикатного анализа проб изверженных горных пород.
Логарифмически-нормальное или логнормальное распределение - представляет собой распределение случайной величины x, логарифм которой h=ln x распределен по нормальному закону, т. е. случайная величина h распределена по нормальному закону с параметрами (mh, s2). Плотность функции распределения:
p(x![]() )=
)=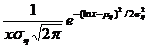 при x>0 и p(x)=0 при x£0.
при x>0 и p(x)=0 при x£0.
Здесь mh и ![]() - параметры распределения, но в отличие от нормального распределения mh и
- параметры распределения, но в отличие от нормального распределения mh и ![]() в условиях логарифмически-нормального распределения не являются параметрами, характеризующими соответственно центр и масштаб кривой плотности вероятностей случайной величины x. Математическое ожидание и дисперсия случайной величины x связаны с параметрами mh и
в условиях логарифмически-нормального распределения не являются параметрами, характеризующими соответственно центр и масштаб кривой плотности вероятностей случайной величины x. Математическое ожидание и дисперсия случайной величины x связаны с параметрами mh и ![]() соотношениями:
соотношениями:

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |




