Математические методы моделирования параметров геологических процессов и явлений (стр. 22 )

Рассмотрим наиболее простой случай, когда функции Fi являются линейными функциями факторов f1, f2, …, fk, т. е.:

где i=1, 2, …, n.

Коэффициент lir называют нагрузкой i-й переменной на r-й фактор. В этом случае основное векторное уравнение можно записать в матричной форме:

Z=Lf+e,

где - матрица факторных нагрузок.

Неизвестными параметрами линейной факторной модели являются факторные нагрузки и дисперсии специфических факторов. Число неизвестных в этой системе, равное nk+n, значительно превышает число уравнений. Поэтому для их оценки прибегают к информации, содержащейся в корреляционной матрице. Из уравнения z=Lf+e легко получить:

,

где R - корреляционная матрица наблюдаемых переменных; Ф - корреляционная матрица общих факторов, которая в предположении некоррелированности факторов становится единичной матрицей; V - ковариационная матрица специфических факторов, являющаяся диагональной. Таким образом, в случае некоррелированных факторов Ф=Е (E – единичная матрица), и мы получаем R=LL'+V.

К числу исходных предпосылок, удовлетворение которых позволяет обоснованно использовать модели факторного анализа в практических исследованиях, относятся следующие.

1. Исходный набор наблюдаемых переменных равноправен с точки зрения причинно-следственных связей, т. е. изменения переменных обусловлены влиянием ряда общих и специфических факторов. Прямая причинно-следственная связь между компонентами вектора отсутствует.

2. Исследуемый набор наблюдаемых переменных подчиняется многомерному нормальному закону распределения. В работе Д. Лоули (1956 г.) показано, что оценки факторных нагрузок, полученные методом максимума правдоподобия, весьма устойчивы даже при существенном отклонении исходного распределения от нормального.

3. Специфические факторы е не коррелированы между собой и с общими факторами.

4. Число общих факторов, наиболее полно определяющее ход изучаемого процесса, должно быть невелико, а именно: число анализируемых переменных должно быть значительно больше предполагаемого числа общих факторов.

5. Корреляционная матрица исходного набора наблюдаемых переменных устойчива от выборки к выборке и допускает разложение R=LL'+V.

6. В исходных наблюдениях отсутствует автокорреляция. Наличие автокорреляции приводит к сокращению объема выборки и не дает возможности эффективно использовать имеющиеся приемы проверки статистических гипотез, так как существенно искажает форму закона распределения выборочных оценок.

7. Выборка исходных данных должна быть представительной.

8. Связь переменных с общими и специфическими факторами является линейной. В противном случае используются нелинейные модели факторного анализа.

Если все перечисленные условия удовлетворяются, то факторный анализ может быть с успехом использован в практических исследованиях. На практике часто возможно и такое его применение, когда эти условия не выполняются. В дальнейшем, используя полученные выводы, можно так модифицировать модель, чтобы требуемые ограничения выполнялись и модель максимально приближалась к реальной ситуации.

Указав общие условия применимости факторного анализа в практических исследованиях, обратимся к вопросу о его применимости в геологии. По-видимому, наиболее трудно удовлетворить условиям пп. 5-7, так как малые объемы выборок и большие размеры корреляционных матриц приводят к неустойчивости результатов вычислений по отношению к изменению объема выборки. Кроме того, наличие коррелированных данных уменьшает и без того малый объем наблюдений, что приводит к большим затруднениям при нахождении собственных значений и собственных векторов матриц, построенных по выборочным данным.

Ниже приводятся два наиболее обоснованных метода факторного анализа.

Метод минимальных остатков Хармана. Факторные нагрузки в методе Хармана определяются из условия минимизации в смысле наименьших квадратов суммы квадратов вне-диагональных элементов остаточной корреляционной матрицы.

Пусть 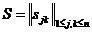- выборочная корреляционная матрица, - искомая матрица факторных нагрузок. Метод Хармана соответствует минимизации нормы матрицы:

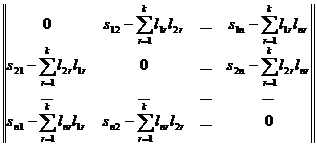
Минимизируемая функция имеет вид:

Цель метода минимальных остатков состоит в том, чтобы, меняя значения факторных нагрузок при фиксированном k, минимизировать функцию f(L) при условии j=1, 2, …, п. Указанное условие вытекает из соотношений для элементов матрицы:

, j=1, 2, ..., n,

где члены соответствуют второй компоненте факторного отображения («факторное отображение» эквивалентно понятию «матрица факторных нагрузок»); - это дисперсия j-го специфического фактора.

Задача нахождения минимума функции f(L) решается методом последовательных приближений.

Метод Лоули и Максвелла. Задача ставится так: используя выборочную корреляционную матрицу наблюдаемой n-мерной случайной величины z=(z1, ..., zn) и предполагая число факторов (k) заданным, дать эффективные оценки параметров lir и элементов vi диагональной матрицы V.

Для решения этой задачи строим функцию правдоподобия:

где N - объем выборки.

Максимум этой функции реализуется при выполнении следующих условий:

где

Полученная система уравнений решается методом последовательных приближений. Задаваясь начальными факторными нагрузками , выбранными произвольно, из первого уравнения находим первое приближение V(1) к матрице V. Затем по матрицам L(1) и V(1) вычисляем первое приближение R(1) к матрице 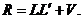Второе уравнение позволяет определить второе приближение к матрице факторных нагрузок L. Следующий шаг делается аналогично и т. д.

Необходимо отметить, что доказательство сходимости итерационного процесса в общем случае отсутствует. В геологии этот метод обычно не применяется.

Центроидный метод. Это метод приближенной оценки факторных нагрузок. В настоящее время используется для получения предварительных наглядных представлений об экспериментальном материале в случае, если он содержит не очень большие объемы численных данных.

Оценка числа факторов. В рассмотренных методах факторного анализа предполагается заранее заданным число факторов k. Приведем критерий оценки числа факторов, принадлежащий Д. Риппу (1953 г.).

Рассмотрим статистику:

В предположении нормальности исходного распределения параметров доказано, что статистика Uk распределена по закону , где число степеней свободы ν равно:

0.5[(n-k)2+(n+k)2].

Если статистика Uk превышает значение при некотором уровне значимости, то гипотеза о том, что число факторов равно k, отклоняется. В противном случае гипотеза принимается. При отклонении гипотезы можно предположить, что модель содержит большее число факторов.

Вращение в пространстве факторов. Остановимся на вопросе о том, однозначен ли выбор факторов в факторном анализе и направлений главных осей в МГК.

Как вытекает из определения собственного вектора, соответствующего наибольшему собственному значению, направление этого вектора является направлением максимального рассеяния выборки, другие направления собственных векторов отвечают следующим по величине характеристикам рассеяния выборки. Такая геометрическая трактовка понятия главных компонент позволяет утверждать, что вращение осей координат после выбора главных направлений производить нецелесообразно. Однако при нарушении условий применимости МГК может случиться, что в конкретной задаче выборка после проектирования на направления первых двух главных компонент будет иметь вид, весьма далекий от эллипса с большой полуосью, совпадающей с направлением первой главной компоненты. Причина такого явления лежит в том, что распределение, из которого взята рассматриваемая выборка, по-видимому, значительно отклоняется от нормального, а может быть, даже является неоднородным по своей структуре, т. е. составлено из разных распределений. В этом случае рекомендует предварительно провести кластерный анализ выборки с целью выделения ее однородных составляющих и затем уже к этим составляющим применять анализ главных компонент.

Если выборка однородна, а выборочный ореол точек не имеет максимального рассеяния по направлению первой главной компоненты, то целесообразно повернуть главные оси на эмпирически выбранный угол так, чтобы новые оси совпадали с направлением максимального рассеяния выборочного ореола.

Рассмотрим вопрос о вращении в пространстве факторов в факторном анализе. Построение матрицы факторных нагрузок L, о которой шла речь выше, в сущности эквивалентно заданию некоторого базиса в пространстве факторов. Предположим, что выбранный базис удовлетворяет условию ортогональности. Если в пространстве факторов выбран другой ортогональный базис, то матрица отображения В, соответствующая новому базису, связана с матрицей отображения L, соответствующей старому базису, следующим преобразованием:

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28