Индикаторные отношения рассмотрены на примере отношения двух элементов-индикаторов: свинца и цинка. В n точках конкретного эрозионного среза первичного геохимического ореола опробованы концентрации свинца xt и цинка - yt, t = 1, 2, . . . , n.
В каждой точке в отдельности находят индикаторные отношения:
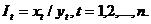
Процедуры интервального оценивания рассматриваемого индикаторного отношения аналогичны пунктам 1, 2, 3, 4, 5, 6. В частности, при согласованности индикаторных отношений с нормальной моделью имеем:
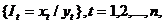 или
или
I1, I2, …, It, …,In;
![]()
![]()
![]()
![]()
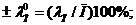
![]()
![]()
где I - неизвестное истинное значение индикаторного отношения свинца к цинку.
Интервальные оценки параметров в корреляционном, регрессионном, дисперсионном анализе приведены в соответствующих разделах.
Глава V. Распознавание образов и дискриминантный анализ
§ 1. Вероятностные методы распознавания образов
Распознавание образов - классификация некоторой группы объектов на основе заданных требований. Под образом понимается некоторая область, заданная в многомерном пространстве.
Требования, определяющие классификацию, могут быть различными, так как в различных ситуациях возникают свои типы классификаций, а именно: в зависимости от цели можно выбрать различные фиксированные множества признаков или всевозможные подмножества в этих множествах, в результате чего одна и та же пара объектов может быть отнесена как к одному и тому же, так и к различным образам.
В геометрической интерпретации под образом понимается область в m-мерном пространстве, вдоль координатных осей которого отложены значения признаков. Описание этой области называется эталоном, а отдельная точка в ней - реализацией образа.
Задачу распознавания образов можно понимать как сопоставление некоторой реализации, относительно которой неизвестно к какому образу она относится, с эталонами. В этом случае реализация сравнивается с эталоном каждого образа и относится к тому или иному образу на основе заранее выбранного критерия соответствия или критерия подобия.
Постановку задачи распознавания образов будем называть детерминистской или вероятностной в зависимости от того пересекаются образы между собой или нет.
Другими словами, ситуация будет детерминистской если в любой точке выборочного пространства с ненулевой априорной вероятностью могут появляться реализации лишь одного образа, и вероятностной - в противном случае.
Необходимо особенно подчеркнуть, что отношение неизвестной (контрольной) реализации к тому или иному образу производится на основании априорной модели, при этом делаются предположения либо о характере распределения генеральной совокупности, либо о возможной структуре множества обучающих и контрольных реализаций, либо о типе допустимых правил принятия решений.
Процессу распознавания предшествует процесс обучения. Существует два различных метода обучения. Первый метод предполагает существование достаточно простых правил, настолько, что их можно четко описать, для того чтобы затем, сообразуясь с этими правилами, получать каждый раз требуемый результат.
Второй метод - метод показов предполагает, что учитель, сам верно классифицирует предъявленные объекты (реализации), не может сформулировать правило, по которому он действует.
Кроме обучения, иногда имеет место самообучение. Оно происходит в отсутствие учителя, когда не поступает информации о том, к какому образу относятся предъявляемые для самообучения эталонные реализации. В этом случае ученик сам определяет схожесть предъявляемых реализаций.
Решающей функцией D называется некоторое правило (соответствие, функция, оператор, функционал и т. п.), которое относит каждую реализацию X к какому либо образу A.
В зависимости от того, какой из трех основных процедурных элементов X, D, A неизвестен, имеется три группы задач, связанных с распознаванием образов:
1) задан список образов A и указаны признаки, по которым эти образы следует отличать друг от друга. Требуется найти такое решающее правило D чтобы распознавание произошло успешно;
2) задан список образов A и тип решающих правил D. Требуется выделить информативную комбинацию признаков, которая обеспечивала бы достаточного количества информации для распознавания;
3) задано множество реализаций или признаков и класс решающих функций. Требуется разделить это множество на некоторое число (заданное или произвольное) однородных областей (классов) (задачи таксономии).
Введем следующие обозначения, принятые при описании различных методов распознавания образов:
A1, A2, …, AS, …A - образы, l - их число, S, r=1, 2, …, l;
x1, x2, …, xi, …, xm - признаки, m - их число, I, j=1, 2, …,m;
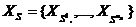
- множество эталонных реализаций S-го образа, S = 1, 2, …, l;
![]() - значение i-го признака в t-й реализации для S-го образа;
- значение i-го признака в t-й реализации для S-го образа;
![]() - значение i-го признака в u-й реализации, u =1, 2, …, N;
- значение i-го признака в u-й реализации, u =1, 2, …, N;
X - реализация, подлежащая распознаванию.
Указанные три группы задач совпадают с основными группами задач, решаемых методами прикладной статистики и лишь слегка переформулированных. В прикладной статистике выделяются три основные задачи, для решения которых применим аппарат математической статистики: задачи классификации объектов, задачи выделения информативных комбинаций признаков и задачи оценивания зависимостей между случайными величинами. Таким образом, методы распознавания образов позволяют решать все основные задачи прикладной статистики, что свидетельствует о широкой применимости их при решении различных геологических задач, начиная от поисковой геологии вплоть до подсчета запасов месторождений полезных ископаемых. Методы распознавания образов были эффективно применены для разделения нефтеносных и водоносных пластов по каротажным данным, определения нефтеносности структур по результатам химического анализа пластовых вод, уточнения связей геохимических показателей с нефтеносностью и битуминозностью, определения перспективных площадей и участков, прогнозной оценки геомагнитных аномалий, идентификации сейсмических волн, определения генетической принадлежности минералов, прогнозирования различных геологических характеристик. Ниже будут рассмотрены основные вероятностные методы распознавания образов, тогда как детерминированные методы («обобщенный портрет» Вапника и Червоненкиса, «Потенциальная функция» , , «Кора-3» , «Тупиковые тесты и тестеры» , , и многие другие) в настоящей работе не приводятся.
Правило Байеса. Рассмотрим случай многих образов и будем считать x1, x2, …, xm случайными величинами, а именно результатами измерения признаков в условиях помех.
Пусть для каждого образа AS, где S = 1, 2, ..., l, известна m-мерная функция плотности вероятности (или распределения) p(X|AS) вектора признаков X, т. е. функция плотности условной вероятности (или распределения) появления в X точек из AS и вероятность p(AS) появления образа AS, где S=1, 2, ..., l. Тогда задача распознавания образов может быть сформулирована как определение решающей функции D = D(X), где D(X) = DS означает, что принимается гипотеза HS: XÎAS.
Потери, когда принято решение DS, т. е. XÎAS (хотя в действительности ХÎАr), обозначим L(Ar, As). Тогда условные потери (или условный риск) для XÎAs равны: r(As, D) = ∫ L(As, D)р{X|As)dx, и для множества р = {р(As)}, S = 1, 2, ..., l, средние потери (средний риск) равны:
![]()
где ![]() - апостериорный условный средний риск решения D при фиксированном x.
- апостериорный условный средний риск решения D при фиксированном x.
Задача заключается в выборе такого решения DS (S = 1, 2, …, l), которое минимизирует средний риск R(p, D) или максимум условного риска r(AS, D).
Оптимальное решающее правило минимизации среднего риска называется правилом Байеса.
Пусть D* - оптимальное решение в смысле минимума среднего риска; тогда:
![]() , т. е.
, т. е.
![]()
Пусть функция потерь:
![]()
Тогда D* = Ds, если:
![]()
для всех r = 1, 2, ..., l.
Пусть λ - отношение правдоподобия для образов Аr и As:
![]()
Тогда D* == Ds, если:
![]()
для всех r = 1, 2, ..., l.
Разделяющей границей между AS и Ar будет:
![]() или
или
![]()
Пусть р(X|AS) функция плотности многомерного нормального распределения с вектором средних Ms и ковариационной матрицей Ks:

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |




