Эту гипотезу об однородности проверяют с помощью статистики:
![]()
которая асимптотически распределена как c2 с (p-1) степенями свободы. Действие фактора считается несущественным (при уровне значимости a), если 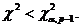
§ 2. Тренд-анализ
Карта - это двумерное представление некоторой области. Большинство карт представляют собой оценки некоторых непрерывных функций по результатам наблюдений в дискретных контрольных точках.
Реализации этих функций (трендов) можно представить в виде некоторых поверхностей в трехмерном пространстве или структурных карт в изолиниях (изолинии на карте связывают точки равных значений, и пространство между "соседними" изолиниями содержит только точки, значения которых находятся внутри интервала, определяемого этими изолиниями). Наиболее широко применяемый метод для построения и анализа карт - тренд-анализ.
Тренд-анализ - математический метод, используемый для исследования закономерностей изменения геологического признака в пространстве. Если исследуются закономерности изменения геологического признака во времени, то существует другое название - анализ временных рядов. Более узкое понимание тренд-анализа: процедура аппроксимации эмпирических данных некоторыми вполне определенными функциями, аргументами которых являются координаты точек наблюдения. Предполагается, что любое из наблюдаемых значений признака z может быть представлено в виде суммы двух компонент, одна из которых (F) рассматривается как неслучайная функция от координат, а другая (j) - как случайная:
z(x)=F(x)+j(x), z(x, y)=F(x, y)+j(x, y),
где x, y - координаты точек наблюдения.
Детерминированная часть F(.) отражает закономерное изменение признака z в пределах исследуемой пространственной или временной области. Обычно такую систематическую составляющую связывают с действием регионального геологического фактора, сфера влияния которого заметно превышает размеры участка аппроксимации.
Появление флуктуации j(.) может быть вызвано следующими причинами: влиянием локально действующих геологических факторов и случайными ошибками измерений признака z.
В зависимости от смысла решаемой геологической задачи внимание исследователя может быть сосредоточено на следующих вопросах:
а) - выявление общей тенденции (тренда) в изменении признака z;
б) - обособление локальной составляющей (поиск положительных и отрицательных аномалий).
1. Выделение региональной составляющей.
Задача решается вполне однозначно лишь в том случае, когда исследователю известны основные параметры процесса, формирующего переменную z. Но чаще всего такая информация отсутствует. Поэтому точное решение задачи недостижимо. Неопределенность можно уменьшить, лишь введя некоторые ограничения на вид аппроксимирующей функции F(.) и функции j(x). На практике при построении тренда используют достаточно простой критерий:
![]()
т. е. норма в функциональном пространстве H не превосходит требуемой точности аппроксимации (e).
Доброкачественность аппроксимации во многом зависит от удачного выбора класса функций H. В геологии чаще всего используются следующие приемы сглаживания:
а) методы, опирающиеся на скользящие средние;
б) аппроксимация алгебраическими полиномами;
в) приближение гармониками и г) сплайн-аппроксимация.
Методы скользящего среднего. В основе этих методов лежит следующая общая процедура.
Для первых m членов (m - нечетно) сглаживаемого ряда объемом n наблюдений (m<n) определяется "сглаженное" значение для точки k=(m+1)/2.
Затем вновь берется m членов, начиная со второго (т. е. производится сдвиг на одно наблюдение), и вычисляется следующее значение.
В простейшем случае сглаживание выполняется обычным усреднением значений z:
![]()
где zk - "сглаженное" значение, относимое к точке k; zt - исходное значение аппроксимируемого признака в точке t.
Часто значения zt вводятся в расчетную формулу с весами Ct, зависящими, в частности, от величины t, определяющей степень удаленности от "центральной точки":
![]()
где S - алгебраическая сумма весовых коэффициентов (нормированный множитель). Причем Ck-i=Ck+i.
Выбор формулы обычно определяется опытным путем. Аппроксимация скользящим средним, подавляя высокочастотную компоненту, сохраняет общую конфигурацию крупных пиков, соответствующих региональной составляющей.
К недостаткам метода относятся:
1 - часто наблюдаемое несовпадение местоположения пиков до и после сглаживания;
2 - отсутствие сглаженных значений на краях аппроксимируемых рядов.
В двумерном случае получаем двумерный тренд:
![]()
где xi, yj - координаты центра площадки ("окна") сглаживания Pij; xr, ys - координаты точек наблюдения, принадлежащих площадке Pij; C(xr, ys) - весовая функция; aij - нормировочный множитель.
Многочисленные модификации метода "скользящего окна", используемые в геологических исследованиях, отличаются друг от друга формой и размерами площадок трансформации, весовыми функциями, требованиями к расположению и количеству точек, охватываемых сглаживаемым окном и т. п. Простейший вариант "скользящего окна" - сглаживание невзвешенным осреднением:
![]()
где m - число наблюдений в пределах площадки Pij.
Этот способ применяется в случае, когда есть основания предполагать, что в границах площадки сглаживания F(x, y)=const, а j(x, y) однородна, распределена нормально и ее значения в соседних точках взаимно независимы. Роль весовых функций можно проиллюстрировать на методе "ближайших точек".
К особенностям метода относятся:
а) размер и форма площадок заранее не определяются;
б) исходные точки могут располагаться неравномерно;
в) число "ближайших точек" m, участвующих в сглаживании, постоянно.
Чтобы построить аппроксимирующую поверхность методом "ближайших точек", вся исследуемая территория покрывается прямоугольной (квадратной) координатной сеткой. Затем вычисляются значения, соответствующие узлам этой сетки. Для этого отыскиваются m ближайших точек к узлу с координатами (xi, yj), затем рассчитываются расстояния между узлом и каждой из этих точек:
![]()
Величина 1/Drs играет роль весовой функции. Нормирующий множитель определяется:
![]()
В результате получаем формулу двумерного тренд-анализа:
![]()
Заметим, что если xi=xr и yj=ys, то аппроксимированное значение совпадает с наблюдаемым значением.
Аппроксимация алгебраическими полиномами. Для всей наблюдаемой совокупности эмпирических данных искомая функция F(.) заменяется полиномами Pl степени l:
![]()
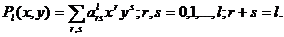
Коэффициенты полинома определяются методом наименьших квадратов из условия:
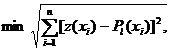
аналогично - для двумерного случая.
Выбор степени полинома является проблемой. Ее однозначное решение требует дополнительной информации о процессах, формирующих исследуемый признак z, которой геолог в подавляющем большинстве случаев не располагает. Обычно стремятся к построению плавно изменяющейся поверхности, задаваемых полиномами невысоких степеней. Но погрешность аппроксимации может оказаться в этом случае недопустимо большой. С повышением же степени полинома все больший вес получают эффекты, связанные с действием локальных факторов. Кроме того, при небольшом числе неравномерно расположенных точек и высоких степенях полинома, возможны неконтролируемые отклонения аппроксимирующей от моделируемой поверхности. Первый признак этого - "краевой эффект", выражающийся в появлении на краях карты чрезмерно высоких и низких значений оценки признака.
Аппроксимация гармониками. Сглаживание эмпирических данных с помощью рядов Фурье (гармонический анализ) уместно в случаях, когда переменная периодически изменяется во времени и (или) пространстве. Такую ситуацию (цикличность) можно ожидать в ситуациях, характеризующихся более или менее регулярной повторяемостью в пределах изучаемого участка земной коры определенного комплекса геологических условий. В одномерном случае периодическую составляющую можно записать в виде ряда Фурье:
![]()
где k - номер гармоники (гармоническое число); l - длина основной волны. Выбор l произволен (обычно - это число равное или превышающее длину исследуемого ряда наблюдений).
Нахождение неизвестных коэффициентов осуществляется методом наименьших квадратов. В двумерном случае схема аппроксимации аналогична. Периодическая составляющая в этом случае записывается в виде двойного ряда Фурье. Трудоемкость вычисления коэффициентов существенно снижается, если точки наблюдений расположены в узлах регулярной сети.
Аппроксимация сплайн-функциями. Приближенное описание геологических поверхностей сплайн-функциями позволяет устранить ряд недостатков, присущих полиномиальной аппроксимации. А именно: снизить трудоемкость вычислительных процедур при моделировании сложных поверхностей полиномами высоких степеней и избежать искажений типа "краевых эффектов" в зонах, удаленных от центра карты и слабо обеспеченных наблюдениями. В то же время сглаживание сплайн-функциями, являясь кусочно-полиномиальной аппроксимацией, сохраняет все преимущества приближения исследуемых геологических полей многочленами низких степеней.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |




