![]()
Коэффициент ковариации между переменными i и l равен:
![]()
Коэффициент ковариации между переменными i и l внутри групп равен:
![]()
Дисперсия между группами i и l равна:
![]() S={sil}
S={sil}
- матрица порядка p*p; W={wil} - матрица порядка p*p; B={bil} -матрица порядка p*p. Тогда: [S]=[B]+[W].
Задача дискриминантного анализа состоит в нахождении множества линейных весов для переменных (вектор A) так, чтобы отношение ![]() достигало максимума. Это отношение достигнет максимума когда A - собственный вектор матрицы [W]-1*[B] соответствующий наибольшему собственному значению. Можно вычислить собственные вектора для каждого положительного собственного значения. Таким образом, мы вычислим последовательность дискриминантных функций, которые дают разделение на заранее заданные группы настолько хорошо, насколько это возможно. В общем случае матрица [W]-1*[B] не является симметричной, поэтому собственные вектора находятся не совсем легко и они не ортогональны.
достигало максимума. Это отношение достигнет максимума когда A - собственный вектор матрицы [W]-1*[B] соответствующий наибольшему собственному значению. Можно вычислить собственные вектора для каждого положительного собственного значения. Таким образом, мы вычислим последовательность дискриминантных функций, которые дают разделение на заранее заданные группы настолько хорошо, насколько это возможно. В общем случае матрица [W]-1*[B] не является симметричной, поэтому собственные вектора находятся не совсем легко и они не ортогональны.
§ 4.Статистические методы разграничения геологических объектов
Это совокупность приемов статистической обработки многомерных данных, которые в итоге приводят к разделению изучаемого набора наблюдений на некоторое заранее неизвестное число статистически однородных, отличающихся друг от друга групп. Для геологии типична ситуация, когда относительно имеющегося набора многомерных наблюдений заранее неизвестно, является ли он однородным, т. е. состоит только из одной группы, или неоднородным, и тогда на какое число однородных групп его следует разделить, и какой состав этих групп. Причем задача разграничения совокупности наблюдений на однородные группы принципиально отличается по своей постановке от дискриминантного анализа, в котором группы априори заданы, тогда как в задаче разграничения они неизвестны и их следует определить. Задача разграничения обычно предшествует дискриминантному анализу. Формально задачу разграничения можно сформулировать как проверку гипотезы:
H0: m1=...=mn=m0
при альтернативе H1: mt¹m0 хотя бы для одного t=1,....,n (n - число наблюдений, mt - неизвестное многомерное среднее).
Если в результате проверки окажется, что следует принять гипотезу H0, то из этого следует, что изучаемый набор измерений разделять на группы нельзя, так как он является однородным. Если же будет принята альтернативная гипотеза H1, то это значит, что рассматриваемый набор наблюдений можно разделить на две или более однородные группы. Путем последовательной процедуры деления неоднородного набора наблюдений на две части достигается разделение на однородные отличающиеся одна от другой группы.
Процедура такого деления базируется на следующих принципах:
1 - каждая группа наблюдений анализируется на однородность;
2 - если группа статистически неоднородна (значение некоторого критерия отличия групп больше допустимого при заданном уровне значимости), то она разбивается на две группы, причем это разбиение производится таким образом, чтобы эти группы максимально отличались друг от друга относительно критерия отличия групп;
3 - если все группы статистически однородные, то процесс деления прекращается.
Однако некоторые из полученных разграничений (разбиений на группы) могут оказаться ложными, и потому для корректного решения задачи разграничения необходимо использовать еще одну процедуру - устранение ложных границ:
1 - для каждой пары полученных групп вычисляется значение критерия их отличия;
2 - выбирается пара групп с минимальным значением этого критерия;
3 - если это значение больше допустимого при заданном уровне значимости, то дальнейшие вычисления прекращаются и все выделенные группы наблюдений рассматриваются как существенно отличающиеся одна от другой; в противном случае эти две группы объединяются в одну и продолжается анализ полученной новой совокупности групп.
Полученные в результате группы наблюдений следует рассматривать как статистически однородные, отличающиеся одна от другой совокупности.
Приведем алгоритм разграничения набора m-мерных наблюдений, расположенных на плоскости или трехмерном объеме.
А. Проверка гипотезы об однородности
1. Дана выборка из n m-мерных наблюдений:
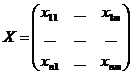 .
.
Множество значений {t|1≤t≤n} будем обозначать через Т.
2. Рассматривается n вариантов разбивки совокупности n наблюдений на две части, причем одна из них содержит только одно наблюдение Xt, а другая - оставшиеся n-1 наблюдений. Для каждого из n вариантов такой разбивки на множества A1 и Аn-1 вычисляется значение критерия:
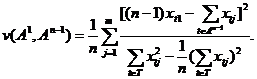
Из всех n значений критерия и v(А1,An-1) выбирается максимальное, чем определяется соответствующее этому максимуму наблюдение Xt={xt1, …, xtm}.
3 Рассматриваются все n-1 пары, образованные Xt и оставшимися n-1 наблюдениями, и соответствующие им n-1 вариантов разбивки пространства T на два подмножества A2 и An-2. Для каждой такой разбивки вычисляются значения критерия, т. е.:
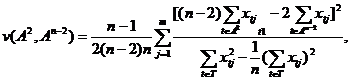
и определяется тот вариант из n-1 вариантов, которому соответствует 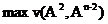 . Таким образом, устанавливается пара наблюдений
. Таким образом, устанавливается пара наблюдений ![]() , включающая
, включающая ![]() выявленное на предыдущем этапе.
выявленное на предыдущем этапе.
4 Эта процедура продолжается до тех пор, пока не будет достигнута разбивка на n/2 наблюдений в случае четного n, и на (n-1)/2 и (n+1)/2 при нечетном n. Таким образом, для любого k≤n/2 при четном n и k≤(n-1)/2 при нечетном n вычисляется значение критерия:
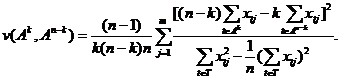
При этом множество Ak включает k-1 наблюдений, обеспечивающих максимальное значение критерия на k-1 предыдущей стадии вычислений.
5. В результате будет получена последовательность n/2 или (n-1)/2 максимальных значений критерия, полученных на n/2 или (n-1)/2 стадиях вычислений. Из всех этих значений выбирается
максимальное, которому соответствует разбивка Т на:
![]() и
и ![]() ,
,
т. е. отыскивается значение:
![]()
где Ak - класс всех множеств, включающих выбранную на предыдущей стадии комбинацию k-1 наблюдений.
6. Если ![]() где
где ![]() заданное значение χ2, соответствующее уровню значимости q и m степеням свободы, то дальнейшие вычисления прекращаются, так как для данного набора наблюдений гипотеза об однородности не отклоняется, из чего следует, что любые разграничения этой совокупности не имеют смысла.
заданное значение χ2, соответствующее уровню значимости q и m степеням свободы, то дальнейшие вычисления прекращаются, так как для данного набора наблюдений гипотеза об однородности не отклоняется, из чего следует, что любые разграничения этой совокупности не имеют смысла.
Если же 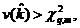 то гипотеза об однородности набора наблюдений отклоняется, из чего следует, что изучаемую совокупность наблюдений нужно разделить не менее чем на две части. При этом выбирается тот вариант разбивки на две части, который соответствует
то гипотеза об однородности набора наблюдений отклоняется, из чего следует, что изучаемую совокупность наблюдений нужно разделить не менее чем на две части. При этом выбирается тот вариант разбивки на две части, который соответствует ![]() .
.
Необходимо отметить, что в практической работе значительно удобнее пользоваться отношением:
![]()
Вычислительные процедуры прекращаются и совокупность рассматривается как однородная, если τ≤3, и гипотеза об однородности отклоняется, если τ >3.
Б. Поиск границ
7. Если гипотеза об однородности изучаемой совокупности наблюдений отклонена, то эта совокупность делится на две части в соответствии с ![]() .
.
8. Каждая из двух новых совокупностей анализируется отдельно по алгоритму, описанному в части А, в результате чего принимается решение об однородности или неоднородности каждой из совокупностей. Если для какой-либо из этих совокупностей гипотеза об однородности принимается, то дальнейшие вычисления для нее прекращаются. Если же принимается альтернатива, то данная совокупность снова делится на две части, в соответствии с правилом, изложенным в п. 7, и анализ вновь полученных совокупностей продолжается.
9. Процедура такого дихотомического деления изучаемой совокупности продолжается до тех пор, пока во всех выделенных более дробных совокупностях не будет принята гипотеза об однородности. Однако некоторые из полученных разграничений могут оказаться ложными, и поэтому нужно перейти к третьей части алгоритма - устранению ложных границ.
В. Устранение ложных границ
10. В результате проведенных вычислений изучаемая выборка, объем которой n, будет разделена на h групп наблюдений. Обозначим через Т1, Т2, ..., Tl, ..., Th - непересекающиеся подмножества в Т, которые соответствуют выделенным группам наблюдений.
11. Из упомянутых h групп наблюдений можно образовать, h(h-1)/2 пар и для каждой из них вычислять значение критерия:
![]()
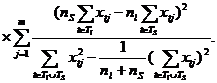
12. Из всех этих значений выбирается минимальное, которое сравнивается с допустимым ![]() при заданном уровне значимости q и m степенях свободы.
при заданном уровне значимости q и m степенях свободы.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |




