F=![]() , если
, если 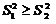 и F=
и F=![]() , если
, если ![]() .
.
В условиях нулевой гипотезы H0:![]() =
=![]() величина F распределена по закону Фишера с k=n1-1 и l=n2-1 степенями свободы. Нулевая гипотеза считается подтвердившейся, т. е. не противоречащей эмпирическим данным, если рассчитанная величина F не превысит допустимого Fa,k, l, соответствующего заданному уровню значимости a при k и l степенях свободы (для случая
величина F распределена по закону Фишера с k=n1-1 и l=n2-1 степенями свободы. Нулевая гипотеза считается подтвердившейся, т. е. не противоречащей эмпирическим данным, если рассчитанная величина F не превысит допустимого Fa,k, l, соответствующего заданному уровню значимости a при k и l степенях свободы (для случая 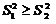 ). Если же вычисленное F превысит критическое (т. е. F>Fa,k, l), то нулевую гипотезу следует отклонить как противоречащую исходным данным и принять альтернативные гипотезы о существенности различий в истинных дисперсиях H1:
). Если же вычисленное F превысит критическое (т. е. F>Fa,k, l), то нулевую гипотезу следует отклонить как противоречащую исходным данным и принять альтернативные гипотезы о существенности различий в истинных дисперсиях H1:![]() ¹
¹![]() и полагать, что степень рассеяния выше у объекта, характеризующегося более высокой выборочной дисперсией S2.
и полагать, что степень рассеяния выше у объекта, характеризующегося более высокой выборочной дисперсией S2.
Критерий Бартлета (параметрический) для проверки гипотез о равенстве дисперсий H0:![]() =
=![]() против набора альтернатив H1:
против набора альтернатив H1:![]() ¹
¹![]() , где
, где ![]() и
и![]() - истинные дисперсии для первого и второго объектов. Для критерия Бартлета условия применения те же, что и для критерия Фишера. Приведем упрощенную схему применения критерия Бартлета. Вычисляется величина:
- истинные дисперсии для первого и второго объектов. Для критерия Бартлета условия применения те же, что и для критерия Фишера. Приведем упрощенную схему применения критерия Бартлета. Вычисляется величина:
![]() где
где
![]() ,
,
![]() N=n1+n2.
N=n1+n2.
В условиях нулевой гипотезы H0:![]() =
=![]() величина M распределена асимптотически по закону Пирсона c2 с одной степенью свободы. Нулевая гипотеза считается подтвердившейся, т. е. не противоречащей эмпирическим данным, если рассчитанная величина M не превысит критического
величина M распределена асимптотически по закону Пирсона c2 с одной степенью свободы. Нулевая гипотеза считается подтвердившейся, т. е. не противоречащей эмпирическим данным, если рассчитанная величина M не превысит критического ![]() для заданного уровня значимости a. Нулевая гипотеза отклоняется как неподтвердившаяся, если значение M превысит критическое
для заданного уровня значимости a. Нулевая гипотеза отклоняется как неподтвердившаяся, если значение M превысит критическое ![]() . В этом случае следует принять альтернативные гипотезы о существенности различий в истинных дисперсиях H1:
. В этом случае следует принять альтернативные гипотезы о существенности различий в истинных дисперсиях H1:![]() ¹
¹![]() и полагать, что степень рассеяния выше у объекта, характеризующегося более высокой выборочной дисперсией S2. Следует отметить, что критическое значение для критерия Бартлета не зависит от объемов выборок. Поэтому он более удобен к применению для задач классификации, где производится сопоставление различных объектов.
и полагать, что степень рассеяния выше у объекта, характеризующегося более высокой выборочной дисперсией S2. Следует отметить, что критическое значение для критерия Бартлета не зависит от объемов выборок. Поэтому он более удобен к применению для задач классификации, где производится сопоставление различных объектов.
Критерий Сиджела-Тьюки или R-критерий (непараметрический) предназначен для проверки гипотез о равенстве дисперсий H0:![]() =
=![]() против набора альтернатив H1:
против набора альтернатив H1:![]() ¹
¹![]() , где
, где ![]() и
и![]() - истинные дисперсии для первого и второго объектов. Статистика Сиджела-Тьюки нечувствительна к нарушению условий нормальности распределения наблюдений, наличию аномальных значений и т. п. Она является полным аналогом статистики Вилкоксона, но проверка осуществляется в этом случае относительно параметра масштаба (дисперсии), а не параметра сдвига (среднего).
- истинные дисперсии для первого и второго объектов. Статистика Сиджела-Тьюки нечувствительна к нарушению условий нормальности распределения наблюдений, наличию аномальных значений и т. п. Она является полным аналогом статистики Вилкоксона, но проверка осуществляется в этом случае относительно параметра масштаба (дисперсии), а не параметра сдвига (среднего).
Учитывая это обстоятельство, можно для проверки нулевой гипотезы H0:![]() =
=![]() пользоваться теми же критическими значениями W1 и W2, что и в случае применения критерия Вилкоксона. Это удобно для практических расчетов при обработке геологических данных.
пользоваться теми же критическими значениями W1 и W2, что и в случае применения критерия Вилкоксона. Это удобно для практических расчетов при обработке геологических данных.
Отличие критерия Сиджела-Тьюки от критерия Вилкоксона заключается в ином характере ранжирования выборочных данных. Номер (ранг) 1 приписывается наименьшему члену вариационного ряда, номер 2 - наибольшему, номер 3 - второму максимальному, номер 4 - второму наименьшему и т. д. Если n1+n2 нечетно, то медианный член устраняется.
Для применения R-критерия Сиджела-Тьюки следует убедиться в равенстве параметров сдвига (равенстве средних); если равенство средних не имеет места, то следует центрировать выборочные данные, например медианами.
Известны две схемы применения рангового критерия Сиджела-Тьюки.
1. С помощью критериев Вилкоксона или Вэлча убеждаемся в равенстве средних для двух сравниваемых объектов. При отсутствии сдвига можно пользоваться исходными данными, в противном случае – наблюдения (анализы проб) в обеих выборках центрируются своими медианами. Дальнейшие операции осуществляются с центрированными данными.
2. Составляется общий вариационный ряд N=n1+n2 в порядке возрастания всех исходных центрированных членов.
3. Вышеупомянутым специальным способом (ранг 1 – наименьшему члену, ранг 2 – наибольшему, ранг 3 – второму наибольшему, ранг 4 – второму наименьшему и т. д.) производится ранжирование всех членов общего вариационного ряда. Если число наблюдений нечетно, то среднее наблюдение (медиана) не получает никакого ранга, если четное – оно получает наивысший ранг.
4. Равным значениям (совпадающим членам) дается скорректированный средний ранг, представляющий собой среднее арифметическое рангов совпадающих членов вариационного ряда.
5. Статистика R-критерия Сиджела-Тьюки - это сумма рангов ri, относящихся к членам меньшей по объему выборки:
R=![]() , где n1£n2.
, где n1£n2.
6. Аналогично процедуре применения критерия Вилкоксона определяют критические значения W1 и W2.
7. Проверяемая гипотеза ![]() принимается как непротиворечащая выборочным данным, если вычисленная статистика R не выйдет за пределы, образованные критическими значениями W1 и W2 (W1 ≤ R ≤ W2), и если статистика R окажется за допустимыми пределами W1 и W2 (R<W1 R>W2).
принимается как непротиворечащая выборочным данным, если вычисленная статистика R не выйдет за пределы, образованные критическими значениями W1 и W2 (W1 ≤ R ≤ W2), и если статистика R окажется за допустимыми пределами W1 и W2 (R<W1 R>W2).
Пункты 1-5 полностью совпадают с пунктами 1-5 схемы А.
6. Для не слишком малых выборок (n1>9 и n2>9) различия в дисперсиях (![]() ) с достаточной точностью определяется с помощью стандартизированной нормальной переменной:
) с достаточной точностью определяется с помощью стандартизированной нормальной переменной:
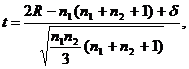
где ![]()
При сильно различающихся объемах выборок n1 и n2 следует пользоваться скорректированным выражением:
![]()
Если пятая часть и более наблюдений связаны равенствами, то формула для t усложняется.
7. Проверяемая гипотеза ![]() принимается как подтвердившаяся, если
принимается как подтвердившаяся, если ![]() , и отклоняется и тем самым принимаются альтернативы
, и отклоняется и тем самым принимаются альтернативы ![]() , если величина |t| превысит допустимое tα/2 (при α=0,05, tα/2=1,96).
, если величина |t| превысит допустимое tα/2 (при α=0,05, tα/2=1,96).
Критерий Джеймса-Сю (параметрический) для проверки гипотез о равенстве многомерных средних в двух объектах. Критерий базируется на предположении о многомерном нормальном распределении случайных величин и отсутствии аномальных наблюдений, а также не предполагает равенства ковариационных матриц. По двум исходным m-мерным выборочным данным {xi} и {yi} объема n1 и n2 соответственно рассчитываются векторы средних арифметических X и Y и оценки ковариационных матриц S1 и S2 по каждой выборке. Рассчитывается оценка обобщенной ковариационной матрицы:
![]()
и статистика Джеймса-Сю:
I=![]() .
.
В условиях нулевой гипотезы о равенстве многомерных средних в двух объектах статистика I асимптотически распределена по закону Пирсона c2 с m степенями свободы. Поэтому, если окажется I£![]() , то для заданного уровня значимости a принимается нулевая гипотеза о равенстве многомерных средних как подтвердившаяся. В противном случае, нулевая гипотеза должна быть отклонена как противоречащая эмпирическим данным и приняты альтернативные гипотезы о существенности различий в многомерных средних сравниваемых двух объектов.
, то для заданного уровня значимости a принимается нулевая гипотеза о равенстве многомерных средних как подтвердившаяся. В противном случае, нулевая гипотеза должна быть отклонена как противоречащая эмпирическим данным и приняты альтернативные гипотезы о существенности различий в многомерных средних сравниваемых двух объектов.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |




