Математические методы моделирования параметров геологических процессов и явлений (стр. 21 )

§ 5. Ковариационный анализ

Ковариационный анализ - статистический метод оценки влияния на случайную величину различных одновременно действующих факторов, одни из которых заданы качественно, а другие могут быть измерены количественно. Иными словами, ковариационный анализ может рассматриваться как комбинация дисперсионного и регрессионного анализов.

Линейная модель ковариационного анализа имеет вид:

где X - некоторые постоянные коэффициенты; b - фиксированные в данном эксперименте факторы; g - коэффициенты регрессии Y на z; z'g - определяет вклад факторов, поддающихся количественному исследованию (z - значения факторов или регрессоров); e - случайная нормально распределенная величина.

Будем полагать, что коэффициенты регрессии не зависят от градаций качественного фактора, задающего разбивку исходных данных на p групп:

g1=…=gp=g.

Основные предположения ковариационного анализа:

1 - Y имеет нормальное распределение с параметрами (X'b, s2I);

2 - Y имеет нормальное распределение с параметрами (X'b+z'g, s2I);

3 - предполагается, что распределение e нормально с параметрами (0,s2).

Исходные данные для ковариационного анализа:

Предположение (1) соответствует нулевой гипотезе:

а предположение (2) – гипотезе:

.

Если гипотеза Hg выполняется, то проверка гипотезы Hb сводится к общему дисперсионному анализу. Если гипотеза Hg отклоняется, то перед проверкой требуется внести некоторые коррективы, исключающие эффект регрессии.

Принципиальную схему ковариационного анализа рассмотрим на примере однофакторного анализа с одним независимым переменным (регрессором):

,

где bi - эффект i-ой градации фактора; gzij - эффект, обусловленный действием z; g - коэффициент регрессии; eij - эффект неконтролируемых факторов; i - меняется от 1 до p; j - меняется от 1 до ni.

Проверка гипотезы Определим суммы квадратов и произведений отклонений, отражающих изменчивость Y и z.

А. Внутри групп (градаций):

,

где и .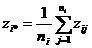

Б. Между группами:

,

где .

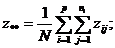
Если гипотеза Hγ верна, то статистика:

имеет F-распределение с 1 и N-p-1 степенями свободы.

Гипотеза о равенстве нулю коэффициентов регрессии g отклоняется, если при выбранном уровне значимости a вычисленное значение критерия превысит табличное Fa,1,N-p-1.

Проверка гипотезы в условиях g ¹ 0. Суммы квадратов "между группами" и "внутри групп" должны быть скорректированы так, чтобы влияние независимой переменной z было исключено.

Для этого вычислим:

a=a1+a2; b=b1+b2; c=c1+c2;

S=b-c2/a; S=b1-(c1)2/a1; S=b2-(c2)2/a2.

Статистика S2/S1 в условиях гипотезы Hb имеет F-распределение с p-1 и N-p-1 степенями свободы.

Эту схему можно обобщить на случаи, когда классификация наблюдений выполнена по двум и более факторам. В геологии ковариационный анализ применяется реже, чем дисперсионный и регрессионный анализ, хотя информация, привлекаемая геологом для решения генетических задач, большей частью носит комбинированный характер.

Глава VI. Главные компоненты и факторный анализ

§ 1. Метод главных компонент

Главными компонентами случайного p-мерного вектора x называются такие ортогональные линейные комбинации vj (j=1,…,r; r£p) составляющих этого вектора (x1,…,xp), что при упорядочении их по дисперсиям выполняются неравенства: S2(v1)³…³S2(vr).

Метод главных компонент (МГК) - статистический метод сжатия информации, основанный на нахождении собственных векторов и собственных значений ковариационной матрицы p-мерного случайного вектора, распределенного по многомерному нормальному закону.

Основная задача, в которой МГК играет важную самостоятельную роль, - задача выяснения сущности геологических процессов по данным изучения современного облика изучаемых объектов. Она сводится к выяснению и оценке роли факторов в становлении изучаемых явлений и существующих закономерностей размещения полезных ископаемых в земных недрах. С ней связаны задачи построения корреляционных моделей в предположении действия определенной совокупности природных процессов, определения особенностей изменения по площади и разрезу составляющих, обязанных действию как отдельно взятых факторов, так и любых их сочетаний. Имеются работы, в которых факторный анализ используется для выделения систематических и случайных составляющих изменчивости комплекса геологических характеристик. Метод главных компонент нашел применение при изучении вопросов становления состава магматических образований, парагенетических ассоциаций и решении ряда других задач.

МГК при решении некоторых задач выполняет также вспомогательные функции в комплексе с другими методами прикладного статистического анализа. Такова его роль в задачах классификации, где он позволяет уменьшить число геологических признаков, в задачах прогнозирования на основе построения регрессионной модели. МГК используется при картировании геолого-геофизических характеристик, при сравнительном изучении природных систем и выделении эволюционирующих составляющих.

Рассмотрим вычислительные аспекты МГК на примере статистического метода Хотеллинга. Пусть x=(x1,…,xp) - p-мерный случайный вектор имеющий многомерное нормальное распределение с математическим ожиданием нуль и ковариационной матрицей S. Можно найти ортогональное преобразование:

v=Ax

такое, что ковариационная матрица случайного вектора v будет диагональной

L=diag(l1,…,lp),

причем l1³…³lp - корни уравнения:

|S-lE|=0,

а j-ый столбец матрицы A удовлетворяет уравнению:

Saj=ljaj.

Этот вектор можно нормировать, так что 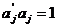и j-ая компонента vj вектора v имеет наибольшую дисперсию среди всех нормированных линейных комбинаций, некоррелированных с предыдущими компонентами v1,…,vj-1.

Обычно ковариационная матрица неизвестна. Ее оценивают выборочной ковариационной матрицей.

Для нахождения значений главных компонент v1,…,vr, r£p, случайного вектора x вычисляются собственные значения l1,…,lp и собственные векторы a1,…,ap матрицы S, причем собственные векторы нормируют к единице.

Далее находят проекции векторов (x1p,…,xkp) на направления главных компонент (a1,…,ap). Тогда v=(x, a) или 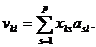Методы регрессионного анализа и распознавания образов позволяют решать задачу уменьшения исходного признакового пространства путем отбрасывания малоинформативных признаков и использования для дальнейшего анализа лишь наиболее существенных. Но при этом, не всегда, достигается наглядное представление исходной информации и обеспечивается учет ее достоверности. Кроме того, вне поля зрения оказываются взаимозависимости между переменными, которая является следствием проявления общих причин и может содержать сведения о природных процессах. В этом отношении определенными преимуществами перед методами регрессионного анализа и распознавания образов обладают компонентный и факторный анализы. Эти методы в определенной степени похожи. Поэтому часть исследователей считают метод главных компонент (МГК) разновидностью факторного анализа (ФА). Но между ними существует и различия.

§ 2. Методы R-модификации факторного анализа

Основоположником факторного анализа считают Ч. Спирмена (1904 г.), который выдвинул предположение о существовании фактора, общего для всех интеллектуальных тестов, и ряда специфических факторов, каждый из которых действует в пределах данного теста и не коррелирует с другими.

Основное положение факторного анализа соответствует интуитивному представлению о том, что признаки исследуемого явления могут быть описаны в терминах небольшого числа основополагающих внутренних параметров - бщих факторов, т. е.:

где i=1, 2, …, n и z(z1, …, zn) – n-мерный вектор-столбец наблюдаемых переменных; Fi - некоторые многочлены переменных f1, f2, …, fk; e=(e1, …, en) – n-мерный вектор-столбец специфических факторов, влияющих только на данную переменную. Предполагается, что они не коррелированы как между собой, так и с общими факторами f. Факторы f1, f2, …, fk обычно предполагаются некоррелированными между собой. Все они имеют определенную интерпретацию.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28