б) составить функцию распределения случайной величины 
и построить ее график;
в) вычислить вероятности попадания случайной величины 
в интервал 
, пользуясь составленной функцией распределения ;
г) составить закон распределения случайной величины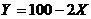 
;
д) вычислить математическое ожидание и дисперсию составленной случайной величины 
двумя способами: пользуясь свойствами математического ожидания и дисперсии, а также непосредственно по закону распределения случайной величины 
Решение:
1) Для вычисления числовых характеристик случайной величины составим расчетную таблицу:
| 10 | 30 | 50 | 70 | 90 |
|
| 0,1 | 0,2 | 0,1 | 0,2 | 0,4 | 1 |
| 1 | 6 | 5 | 14 | 36 |
|
| 10 | 180 | 250 | 980 | 3240 |
|
= 62
Таким образом:
– математическое ожидание по определению равно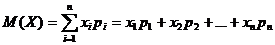 
, или 
;
– дисперсию 
определим по формуле 
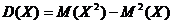, или 
;
– среднеквадратическое отклонение 
по определению равно 
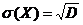, или 
;
2) Для составления функции распределения воспользуемся ее определением
и свойствами: если возможные значения случайной величины принадлежат интервалу 
, то
,если 
, 
, если 
. Таким образом, интегральная функция имеет вид:
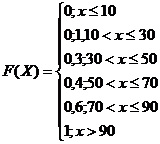
График интегральной функции дискретной случайной величины X рис1.
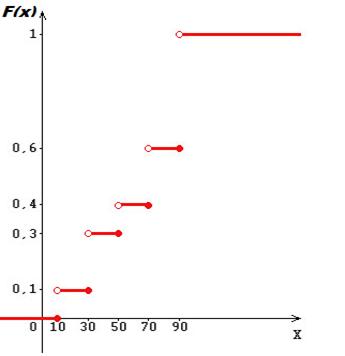
Рис 1. График интегральной функции дискретной случайной величины X
3) Вероятности попадания случайной величины в интервал 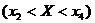вычислим по формуле 
. В данном случае 
, следовательно 
;
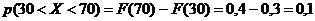4) Составим закон распределения случайной величины 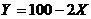. Для этого найдем все возможные значения случайной величины 
:
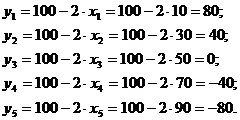
Вероятности 
, с которыми принимает свои возможные значения, равны вероятностям 
, т. е.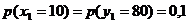 
и т. д.
Таким образом, учитывая, что в законе распределения должно соблюдаться условие ранжирования случайной величины от меньшей к большей, для случайной величины имеем:
| -80 | -40 | 0 | 40 | 80 |
| 0,4 | 0,2 | 0,1 | 0,2 | 0,1 |
5) Вычислим математическое ожидание и дисперсию составленной случайной величины :
– пользуясь свойствами математического ожидания и дисперсии, найдем 
, 
для величины :
;
– непосредственно по закону распределения случайной величины . Составим таблицу для вычислений 
и 
:
| -80 | -40 | 0 | 40 | 80 |
|
| 0,4 | 0,2 | 0,1 | 0,2 | 0,1 | 1 |
| -32 | -8 | 0 | 8 | 8 |
|
| 2560 | 320 | 0 | 320 | 640 |
|
Таким образом:
– математическое ожидание равно 
;
– дисперсию определим по формуле 
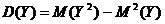, или 
.
Задача 2. Случайная величина задана интегральной функцией распределения . Требуется:
1) убедиться, что заданная функция является функцией распределения некоторой случайной величины, проверив свойства .
В случае положительного ответа найдите:
2) дифференциальную функцию 
;
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
Основные порталы (построено редакторами)